Clasificación de ángulos
Contenido
- Clasificación de los ángulos según su medida: ángulo recto, ángulo agudo, ángulo obtuso
- Clasificación de los ángulos según su posición relativa: ángulos consecutivos, ángulo adyacentes, opuestos por el vértice
- Clasificación de los ángulos según su suma: ángulos complementarios, ángulos suplementarios.
Clasificación de los ángulos
Los ángulos se pueden clasificar según su medida, según su posición y según su suma.
Clasificación de los ángulos según su medida
Según su medida los ángulos se clasifican en convexos y cóncavos.
Un ángulo es convexo cuando su medida es menor de 180°.
Un ángulo es cóncavo cuando su medida es mayor de 180°.
Nota: El ángulo que mide 180° recibe el nombre de ángulo llano y el ángulo que mide 360° recibe el nombre de ángulo de una vuelta.
Los ángulos convexos a su vez se clasifican en ángulo agudo, ángulo recto y ángulo obtuso.
En la figura se muestran tres ángulos:
- El ángulo ABC () es agudo. Su medida es 50°
- El ángulo DEN () es recto. Su medida es 90°
- El ángulo OPQ () es obtuso. Su medida es 120°
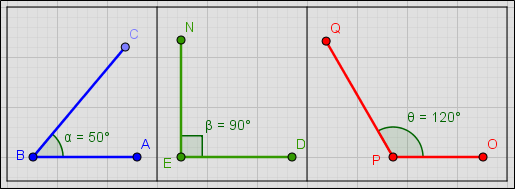
Ángulo agudo es el ángulo cuya medida es menor de 90°.
Ángulo recto es el ángulo cuya medida es igual a 90°.
Ángulo obtuso es el ángulo cuya medida es mayor de 90° pero menor de 180°.
En el applet que sigue, modifique la medida del ángulo para obtener un ángulo agudo, un ángulo recto o un ángulo obtuso.
Clasificación de los ángulos según su posición relativa
Según su posición los ángulos se clasifican en consecutivos, adyacentes y opuestos por vértice.
Ángulos consecutivos: Son dos ángulos que tienen un lado y el vértice común.
En el applet siguiente se muestra el ángulo , ángulo BAC. En él, cuando se activan las dos casillas de verificación, el ángulo se divide en dos: ángulo (ángulo BAF) y ángulo (ángulo FAC). Estos dos ángulos tienen el mismo vértice (A) y comparten un lado (FA) y por eso son consecutivos. La suma de las medidas de los dos ángulos equivale a la medida del ángulo original.
Si el ángulo original es ángulo llano, los ángulos y , además de ser consecutivos, son adyacentes.
Ángulos adyacentes: Son dos ángulos consecutivos que los lados no comunes son semirectas opuestas. En otras palabras, tienen un lado y el vértice común y el lado no común del segundo, es la prolongación del lado no común del primero.
La suma de las medidas de dos ángulos adyacentes siempre es 180°. Est se puede escribir:
Ángulos opuestos por el vértice: Son dos ángulos que tienen el vértice común y sus lados son semirrectas opuestas.
En el applet siguiente se puede apreciar que los ángulos y son opuestos por el vértice: la semirrecta OA es opuesta a la semirrecta OC. De la misma manera, OB es opuesta a OD.
También se puede apreciar que la medida del ángulo es igual a la medida del ángulo . Por qué?
Porque dos ángulos opuestos por el vértice son congruentes, es decir, tienen igual medida
Una forma sencilla de explicar esta propiedad es que los dos son adyacentes al mismo ángulo.
Se recuerda que la medida de dos ángulos adyacentes suman 180°. También, que si dos ángulos son adyacentes, también son suplementarios.
y
como las dos expresiones son iguales a 180°, se tiene que . Por lo tanto,
Clasificación de los ángulos según su suma
Según su posición los ángulos se clasifican en ángulos complementarios y ángulos suplementarios.
Ángulos complementarios: Son dos ángulos que la suma de sus medidas es 90°, es decir, un ángulo recto.
Complemento de un ángulo es la medida que le falta al ángulo para ser un ángulo recto. Así por ejemplo, el complemento de un ángulo de 40° es 90° - 40° = 50°.
Los ángulos complementarios pueden ser consecutivos o no consecutivos como se muestra en los dos applets siguientes.
Desplace el dial del deslizador a para modifcar la medida del ángulo a.
Se observará que al hacerlo también se modifica la medida del ángulo b. La suma de las dos medidas equivale a 90°.
Ángulos suplementarios: Son dos ángulos que la suma de sus medidas es 180°, es decir, un ángulo llano.
Suplemento de un ángulo es la medida que le falta al ángulo para ser un ángulo llano.
Un ejemplo: El suplemento de un ángulo de 40° es 180° - 40° = 140°.
Los ángulos suplementarios también pueden ser consecutivos o no consecutivos. En los dos applets siguientes se muestran estos dos casos.
Desplace el dial del deslizador d para modifcar la medida del ángulo d.
Se observará que al hacerlo también se modifica la medida del ángulo e. La suma de las dos medidas equivale a 180°.