Gaussova eliminace
Řešte soustavu lineárních rovnic o třech neznámých (Matematika I, str. 107)
x + y + z = 3
x + y - 3z = -1
x + 2y - 3z = 1
2x + y - 2z =1
Obrázek v tomto případě není příliš průkazný. I když nejsou žádné dvě roviny rovnoběžné, mohlo by se stát, že všechny sdílejí jeden společný bod.
Počet řešení je na první pohled patrný, použijeme-li příkaz SchodovityTvar na matici rozšířenou i o pravé strany.
Výsledná matice Ael je jednotková, její hodnost je 4. Matice soustavy bez pravých stran má hodnost 3, tedy dle Frobeniovy věty soustava nemá řešení. To je zřejmé i z rozepsání matice Ael do soustavy lineárních rovnic (poslední sloupec je absolutní člen).
x = 0, y =0, z = 0, 0 = 1.
Z poslední rovnice je patrné, že rovnice řešení nemá.
Stejný výsledek obdržíme i použitím online kalkulátoru Wolfram Alpha - viz příkaz Linear System.
Příklady k samostatnému procvičování
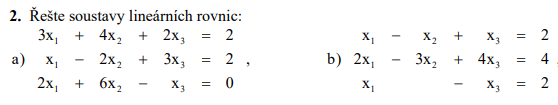
Řešení
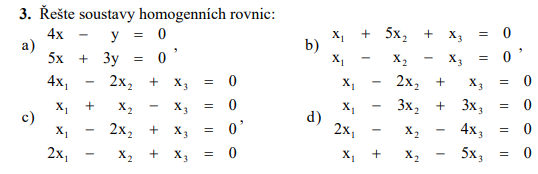
Řešení
