匀变速直线运动的基本规律
物体的运动既是一种时间上的变化，也是一种空间上的变化。
位置、瞬时速度、瞬时加速度都是物体在这个过程中的状态。
描述一个物体的运动，就是揭示物体的状态会如何随着时间和空间变化。
从时间上来说，物体在每个时刻都有自己对应的位置、瞬时速度、瞬时加速度。
从空间上来说，物体在每个位置上都有自己对应的瞬时速度和瞬时加速度。
匀变速直线运动的加速度不变，每个时刻或位置的加速度都是一样的，不需要探究。
接下来我们就探究匀变速直线运动中瞬时速度、位置随着时间怎样变化以及瞬时速度怎样随着位置变化。
一、匀变速直线运动的速度-时间规律
1、公式的推导
我们先来看两个简单的问题：
1.一棵树高1.5m，今后每年长高0.5m，10年后这棵树多高？
10年后这棵树高:1.5m+0.5m/年x10年=6.5m。
2.小明现在有100元钱，是他通过每天攒1元攒的，一个月前他有多少钱?
一个月前小明的钱：100元-1元/天x30天=70元
我们想知道物体在某个时间的状态，通常结合现在的状态和物体在这段时间内的变化去推断。
匀变速直线运动的加速度一直不变就意味着速度变化是可预知的。
只要知道初速度和加速度，我们就可以利用末状态=初状态+变化量这一思想来计算出任意时刻的速度。
2、公式的含义
①物理含义
告诉我们：只要知道物体初始的速度、速度变化率、运动的时间，就可以预测时刻的速度会变成多少。
例1：一汽车以20m/s的速度匀速行驶，因看到前方有障碍物以2m/s2的加速度刹车，刹车过程中加速度不变，求这辆汽车在8s末的速度。
解析：
我们假设汽车行驶方向为正，则，，
根据速度时间规律,8s末的速度
反过来说，若我们知道物体此时的速度为、加速度为，已经运动了时间，也可以推导出初始时的速度。
例2：一汽车以2m/s2的加速度刹车，经过8s停下，求这辆汽车在5s末的速度。
解析：
假设汽车行驶方向为正，，汽车在8s末的速度。
由速度时间规律可得：
代入数据解得：
②数学含义
在数学上，是一次函数，叫常数项或纵截距，叫一次项系数或斜率。
匀变速直线运动的速度和时间是一次函数关系，反过来说，速度和时间成一次函数关系的运动也一定是匀变速直线运动。
例1：一物体运动的速度大小和时间满足关系式，则这个物体做匀变速直线运动，初速度为，加速度。
二、匀变速直线运动的位移-时间规律
1、公式的推导
我们借助图像，来推导匀变速直线运动的位移随着时间的变化规律。
2、公式的含义
①物理含义
这个公式里面，表示的是物体在这段时间内走的位移，而不是物体时刻的位置。
这个公式告诉我们：知道物体的初速度和加速度，就可以计算任意时间物体的位移。
例1：汽车以20m/s的速度做匀速直线运动，看到前方有障碍物立即刹车（反应时间不计），刹车后加速度大小为5m/s2，求汽车刹车后2s内的位移。
解析：
设汽车运动方向为正方向，，。
汽车停下来的时间>，汽车2s时仍在运动。
由位移时间规律，汽车2s内的位移
当然，通过解一元二次方程，这个式子反过来也可以告诉我们物体运动通过一段位移所需要的时间是多少。
例2：一汽车以速度行驶至一危险路段，踩油门以的加速度加速通过，已知危险路段长，求汽车通过该路段的时间。
解析：
由位移时间规律有，代入数据得到（此处将具体方程列出是为了便于大家理解运算过程，这里省略单位，以下皆同）
解这个一元二次方程：或，时间不能为负，舍去。
故通过该地段所需时间为。
例3：列车进入隧道需要减速。一长的列车以的速度驶入长的隧道，进入隧道的一瞬间，列车以大小的加速度做匀减速直线运动，直至列车完全出隧道。求列车通过隧道的时间。
解析：
以列车运动方向为正方向，。
由位移时间规律有，代入数据得到
解得,
列车不可能有两个通过隧道的时间。
我们将代入到速度时间规律里得到，很明显，列车速度不可能反向，故舍去。
即列车通过隧道的时间为。
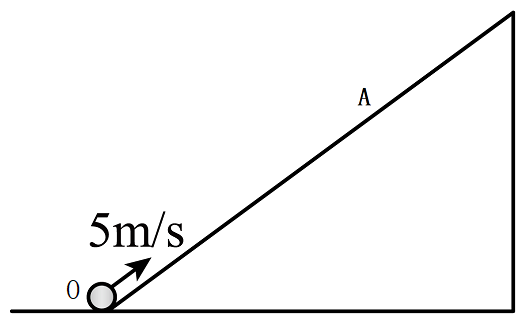
例4：如图所示，
时刻，小球以的速率从固定斜面的底端O点沿斜面向上做匀变速直线运动，加速度大小为，已知OA距离,求小球两次经过A点的时间间隔。
解析：
我们取沿斜面向上为正方向，.
由位移时间规律有，代入数据得
解得
则小球两次经过A点的时间间隔
在以上三个例子中，注意解出来的时间什么时候是有效的，什么时候是无效的，需要结合实际的情景去判断。
时刻，小球以的速率从固定斜面的底端O点沿斜面向上做匀变速直线运动，加速度大小为，已知OA距离,求小球两次经过A点的时间间隔。
解析：
我们取沿斜面向上为正方向，.
由位移时间规律有，代入数据得
解得
则小球两次经过A点的时间间隔
在以上三个例子中，注意解出来的时间什么时候是有效的，什么时候是无效的，需要结合实际的情景去判断。②数学含义
是不含常数项的二次函数，其二次项系数为，即加速度的一半，一次项系数为，即初速度。
若一个物体的位移和时间为二次函数关系，这个物体做匀变速直线运动。从关系式可以反推得到初速度和加速度的信息。
例1：一个做直线运动的物体的位移和时间满足关系：，则这个物体做匀变速直线运动，它的初速度，加速度。
二次函数的图像是抛物线，若一个物体的位移-时间图像是过原点的抛物线，说明它做匀变速直线运动，我们可以根据图像得到解析式，然后再找出它的初速度和加速度。
例2：一运动物体的位移-时间图像如图所示，是过原点的一条抛物线。
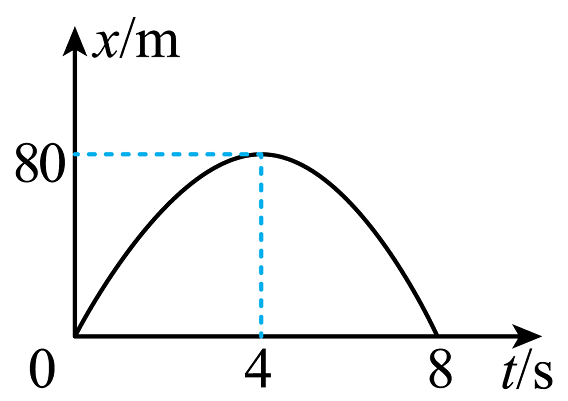由二次函数知识和图中数据我们可以得到位移x和时间t之间的解析式为：，表明物体做匀变速直线运动，运动的初速度为，加速度
由二次函数知识和图中数据我们可以得到位移x和时间t之间的解析式为：，表明物体做匀变速直线运动，运动的初速度为，加速度
———————————————————————————————————————————————
如果我们想表示物体的位置，可以在位移的基础上加上初始的位置。
这个公式表示的就是物体在时刻的位置了。
例3：表示物体以，从初始位置为处开始运动。
此处表示的是物体在坐标系里的位置。
例4：一运动物体的位置-时间图像如图所示，是一条抛物线。
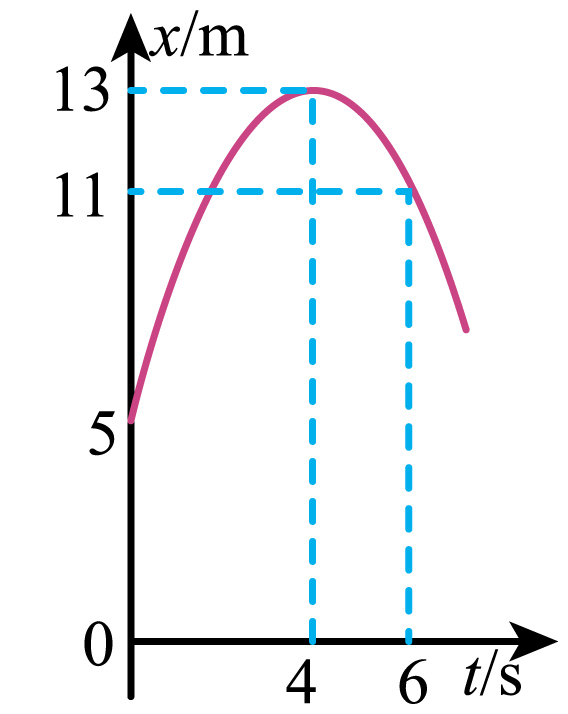由二次函数知识和图中数据，我们可以得到和之间的解析式为：
则物体做匀变速直线运动，加速度，初速度，初始位置。
由二次函数知识和图中数据，我们可以得到和之间的解析式为：
则物体做匀变速直线运动，加速度，初速度，初始位置。③图像
我们将左右两边同时除以时间t，可以得到。
是物体运动位移，是运动时间，表示物体在t时间内的平均速度。
图像反映的是平均速度和时间的关系，不要和表示瞬时速度的图像混为一谈。
我们读这种图像和读其他图像是一样的，关注它的斜率和截距。从表达式中可以看到，斜率是，即加速度的一半，纵截距是初速度。
例1：某汽车在平直公路上做刹车运动，汽车在刹车过程中位移和时间的比值
与时间t之间的关系图像如图所示，下列说法正确的是（ ）
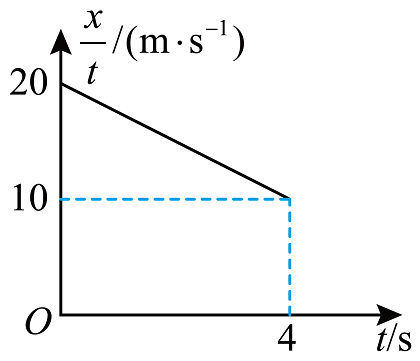
解析：
图像的斜率为，纵截距为20，该车的初速度为，加速度为。B错。
4s时，汽车速度，汽车此时已经停下，A、C均错。
汽车4s已经停下，8s走的位移(注意的物理意义是平均速度，我们可以直接用平均速度x时间来计算出位移)
与时间t之间的关系图像如图所示，下列说法正确的是（ ）
A． 时，汽车的速度为 |
B．该汽车的速度变化率大小为 |
| C．时，汽车的速度为开始刹车时速度的一半 |
| D．从开始刹车时计时，经过8s时间，汽车的位移为40m |
三、匀变速直线运动的速度-位移规律
1、公式的推导
联立前面所学的两个公式：
①
②
我们想要知道的是速度对应于位移的关系，时间不应该出现在我们的公式里。
由①变形得到： ③
代入消元，将③代入②中：
化简得：
即
或者我们可以利用图像来推导：
2、公式的含义
①物理含义
我们将速度-位移公式稍加变形，得到，这个式子告诉我们，只要知道加速度和初速度，就可以预测物体移动位移为时的速度。
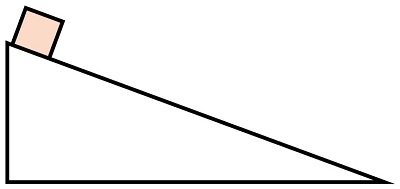
例1：如图所示，一木块从光滑斜面顶端静止释放，下滑加速度为，斜面长，求木块滑至斜面底端时的速度。
解析：
由速度位移规律，，
解析：
由速度位移规律，，反过来说，，若我们知道现在的速度为，加速度为，就可以推测出位移之前的速度为。
例2：某型号航空母舰上装有帮助飞机起飞的弹射系统，已知某型号的飞机在平直跑道上加速时可产生的最大加速度为5m/s2，飞机跑道长160m，当飞机的速度达到50m/s时才能离开航空母舰起飞，设航空母舰始终处于静止状态。求：若要求该飞机滑行160m后起飞，弹射系统必须使飞机具有多大的初速度？
解析：
由速度位移公式，
告诉我们，若物体加速度为，则它从速度变化到所需要经历的位移是。
例3：一汽车正匀速行驶，速度大小为15m/s，突然看见前方40m处有一障碍物后刹车，刹车时获得的加速度大小为3m/s2，汽车是否会撞上障碍物？
解析：
以汽车行驶方向为正，，
由速度位移公式，
汽车从开始刹车到停下的位移<
故不会撞上。
告诉我们，若已知物体从速度变化到所需要经历的位移是，通过此式可以计算出物体的加速度。
例4：某驾驶员驾车以v1=20m/s的速度在水平路面上做匀速直线运动，从发现制动信号到最终停下来，总运动距离为s=50m，忽略反应时间，求该汽车制动过程中的加速度a的大小；
解析：
由速度位移规律，,
速度-时间公式和速度-位移公式分别从时间和空间的角度揭示了物体的瞬时速度会怎么变化，本质上是一样的。
②图像
由公式,我们可以知道匀变速直线运动的和是一次函数关系，纵截距为，斜率为。
图像反映瞬时速度随着位移会如何变化。
此处注意，我们寻找的是和之间的关系而不是和之间的关系，因为图像是一条曲线，不方便我们处理。
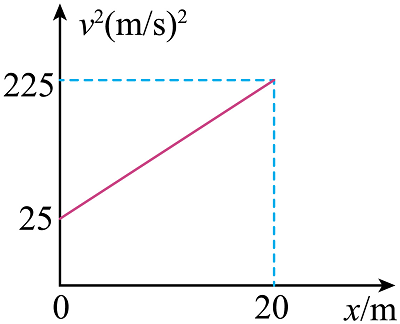
例1：一辆小汽车在长为20m的平直桥面上提速，如图为小汽车在该段桥面上车速的平方（
）与位移（）的关系图，如小汽车视为质点，则小汽车通过该段桥面的加速度大小和时间分别为（ ）
解析：
纵截距为25，,斜率为，加速度。
末速度,通过时间
答案选B、D
）与位移（）的关系图，如小汽车视为质点，则小汽车通过该段桥面的加速度大小和时间分别为（ ）
A． | B． | C． | D． |