Å "Kvadrere" ulike figurer
Matematikere i gamle Hellas, særlig på Euklids tid (ca. 300 f.Kr.), prøvde å løse problemer ved hjelp av linjal og passer. For eksempel ville de finne et kvadrat som har nøyaktig samme areal som et rektangel.
Dette var en del av en større tradisjon der man prøvde å "kvadrere" ulike figurer, altså lage kvadrater med samme areal som andre former.
Aktivitet
Hvordan kan vi bruke en linjal og passer til å lage et kvadrat som har samme areal som et gitt rektangel? Hva tror dere vi må vite om rektangelet for å klare det?
Til undring: Sirkelens kvadratur
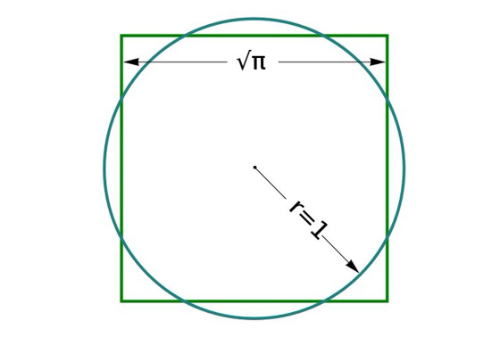
Historien om sirkelens kvadratur er en av de mest kjente og fascinerende utfordringene fra antikkens matematikk. I antikkens Hellas prøvde matematikere å finne en måte å lage et kvadrat med samme areal som en sirkel, kun ved hjelp av linjal og passer. Dette ble kalt "sirkelens kvadratur." Problemet viste seg å være umulig å løse. Hvorfor tror du det?
Om du lurer på om det er mulig å lage en sirkel med akkurat samme areal som et kvadrat, så kan du se på denne og vurder selv: Sirkel og kvadrat med likt areal? – GeoGebra