Extremwertaufgaben darstellen
Extremwertaufgabe 1
Aufgabe 1
Unser Ziel ist heute, Extremwertaufgaben und ihre Nebenbedingungen gleichzeitig grafisch und geometrisch Darzustellen, indem wir zwei Grafikansichten miteinander verbinden. Lies dir dazu erst den Text der Aufgabe von oben durch. Die Nebenbedingung ist hier schon gegeben.
1. Klicke auf das Menü (die drei Striche oben Rechts im Bild) und wähle den Reiter Ansicht aus. Klicke die Kästchen bei den Punkten Algebra, Grafik und Grafik 2, so dass Häkchen in den Kästchen erscheinen. Es sollten nun drei Felder (inkl. Eingabefeld) nebeneinander erscheinen.
2. Verschiebe den dicken Balken zwischen den Feldern, so dass du alle drei einigermaßen gut sehen kannst. Du hast nun eine zweite Grafik erstellt, die aber mit Grafik 1 verbunden ist. Möchtest du einen Punkt oder eine Funktion in eine der zwei Grafiken einfügen, so musst du vorher auf die entsprechende Grafikansicht klicken und erst anschließend im Eingabefeld deinen Befehl eingeben.
Jede Grafik hat oben rechts im Bild eigene Einstellungen, mit denen man Koordinatenachsen und Gitterlinien aktivieren kann (aktiviere diese).
3. Wir starten damit, dass wir in der linken Grafik unser Problem geometrisch darstellen. Erstelle einen Schieberegler für u von 0 bis 3. Klicke zuerst auf die linke Grafik und definiere dann die Nebenbedingung im Eingabefeld
4. Erstelle den Punkt P(u,v(u)). Diesen kannst du nun auf dem Graphen verschieben.
5. Erstelle ein Vieleck aus den Punkten P, (0,v(u)), (0,0) und (u,0). Du hast nun das Rechteck aus der Aufgabe erstellt, dessen Flächeninhalt maximiert werden soll. Wenn du den Punkt P verschiebst oder u änderst, so ändern sich auch die Seiten des Rechtecks.
6. Gib die Fläche des Rechtecks im Schaubild an, indem du oben in der Menüzeile den Punkt Fläche 
auswählst und auf das Rechteck klickst.
7. Nun wollen wir den Flächeninhalt maximieren. Dazu formulieren wir zuerst die Zielfunktion, indem wir die Nebenbedingung in die Extremalbedingung () einsetzen. Diese lautet dann . Klicke zunächst auf die rechte Grafikansicht und gib schließlich die Funktionsvorschrift im Eingabefeld ein. Der Graph für den Flächeninhalt sollte nun in der rechten Grafik erscheinen. Schränke jetzt die Funktion noch auf den für uns interessanten Definitionsbereich [0,3] ein, indem du den Befehl Funktion(Funktion, Startwert, Endwert) verwendest.
8. Erstelle einen Punkt B(u,A(u)). Bewegst du nun den Punkt P, so bewegt sich der Punkt B und andersherum. Bewegst du nun den Punkt B an das Maximum der Flächeninhaltsfunktion, so kannst du sehen wie das Rechteck mit dem größten Flächeninhalt, welches die Nebenbedingung erfüllt, aussieht.
9. Um das Maximum genauer zu bestimmen, verwende den Befehl Extremum(Funktion).
10.(optional) zur Besseren Darstellung kannst du in der rechten Grafik noch die Ableitungsfunktion einzeichnen und einen Punkt S(u,A'(u)) hinzufügen, welcher die Nullstelle der Ableitung anzeigt wenn der Flächeninhalt maximal wird. Applet zu Aufgabe 1
Wie lautet der maximale Flächeninhalt für das Rechteck aus Aufgabe 1? (in )
Aufgabe 2
Mittlerweile sind deine Geogebra Skills für selbstständiges Arbeiten sehr gut ausgereift. Im folgenden Bild befindet sich eine Extremwertaufgabe mit Nebenbedingungen. Stelle die Extremalbedingung und die Nebenbedingungen, als auch die Zielfunktion auf. Stelle die Aufgabe anschließend ähnlich wie in Aufgabe 1 dar und bestimme die Lösung so graphisch. Achte dabei auf den Definitionsbereich. Die gestellten Fragen nach der Aufgabe sollen als Tipps gelten
Extremwertaufgabe
In einer parabelförmigen Giebelwand (Skizze unten) soll ein rechteckiges Fenster eingelassen werden, welches bis zum Boden reicht. Der Giebel ist 4m hoch und 8m breit. Welche Maße muss das Fenster haben, damit die Fensterfläche maximal ist? Wie groß ist die Fensterfläche?
Skizze
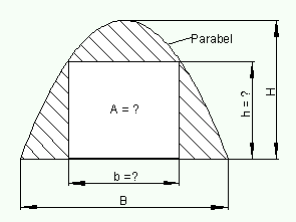
Wie lautet die Extremalbedingung?
Wie lautet die Nebenbedingung?
Wie lautet die Zielfunktion?
Wie groß ist die Maximale Fensterfläche?
Wie groß sind die Seiten dann?