竖直上抛运动
一、竖直上抛运动的基本规律
我们把物体以一定的初速度竖直向上抛出，物体在只受重力作用下的运动就叫竖直上抛运动。物体竖直上抛过程中只受重力的影响，加速度为重力加速度。
以竖直向上为正方向，则加速度为。
我们在处理竖直上抛运动问题时，可以分段去处理，也可以直接全程去处理。
二、竖直上抛运动的对称性
假设物体运动到最高点的时间为，这段时间，物体可以看成逆向的自由落体运动；这段时间，物体做自由落体运动。
从全程来看，物体两次经过某点A时的时间和速度会关于最高点呈对称性。
三、竖直上抛运动的典型问题
1、基本规律的运用
例1：（多选）某物体以30m/s的初速度竖直上抛，不计空气阻力，取向上为正方向，g取10m/s2，则5s内物体的（ ）
解析：
直接以全程运动去处理，
，B正确；
,D正确
，C错误；
路程需要分段去看：
竖直上升阶段
自由下落阶段
自由下落位移
路程，A正确
选ABD。
例2：升降机以速度
匀速竖直上升，升降机内的天花板上有一个螺丝帽突然松脱，脱离天花板。已知升降机天花板到其地板的高度为
。求：
(1)螺丝帽上升的时间；
(2)螺丝上升至最高点时，螺丝与升降机的地板之间的距离
(3)螺丝帽落到地板上时，升降机的地板上升的位移。（本题
）
解析：
螺丝帽突然脱落不会马上做自由落体运动，它会因为惯性继续往上运动一段，等效于竖直上抛运动。
以向上为正方向。
（1）上升时间
（2）螺丝上升至最高点时，对地位移
地板向上位移
此时和螺丝帽和地板距离
（3）假设螺丝落到地板的时间是t，螺丝帽的位移
地板的位移
由题知：
代入解得：
| A．路程为65m | B．位移为25m |
| C．速度改变量为50m/s | D．平均速度为5m/s |
匀速竖直上升，升降机内的天花板上有一个螺丝帽突然松脱，脱离天花板。已知升降机天花板到其地板的高度为。求：
(1)螺丝帽上升的时间；
(2)螺丝上升至最高点时，螺丝与升降机的地板之间的距离
(3)螺丝帽落到地板上时，升降机的地板上升的位移。（本题）
解析：
螺丝帽突然脱落不会马上做自由落体运动，它会因为惯性继续往上运动一段，等效于竖直上抛运动。
以向上为正方向。
（1）上升时间
（2）螺丝上升至最高点时，对地位移
地板向上位移
此时和螺丝帽和地板距离
（3）假设螺丝落到地板的时间是t，螺丝帽的位移
地板的位移
由题知：
代入解得：对于距离抛出点一段距离的问题，注意其多解性。
例3：在一个足够深的井口正上方将一个小球以初速度竖直上抛，不计空气阻力，则经过多长时间小球能够到达距离抛出点的地方（重力加速度g取）（ ）
解析：
以向上为正，假设经过时间t后在抛出点上方5m处，则有
代入解得：或
若物体在抛出点下方5m，则有
解得或(舍去)
故选ACD。
| A．1s | B．3s | C．s | D．2s |
对连续两次经过同一点的，要善于利用竖直上抛运动的对称性。
例4：一个从地面竖直上抛的物体，它两次经过一个较低的点 的时间间隔是，两次经过一个较高点 的时间间隔是，重力加速度为，求、 之间的距离.
解析：
根据时间的对称性，物体从 点到最高点的时间为，从点到最高点的时间为
点到最高点的距离
点到最高点的距离
故、之间的距离为
2、类竖直上抛运动
对于球以一定初速度滚上光滑斜面的问题，其规律和竖直上抛运动类似，只是加速度不为。
例1：(多选)一物体以 的初速度在光滑斜面上向上匀减速运动，其加速度大小为，设斜面足够长，经过 时间物体位移的大小为，则时间可能为( )
A.1s B.3s C.4s D.
解析：
以沿斜面向上为正方向，。
当物体的位移为 时，
解得
当物体的位移为时，
解得
故ACD 正确.
3、竖直上抛运动与自由落体运动的追及相遇
例1：一长为L的金属管从地面以v0的初速度竖直上抛，管口正上方高h处有一小球同时自由下落，金属管落地前小球从管中穿过。已知重力加速度为g，不计空气阻力，不考虑金属管落地后的反弹，问：
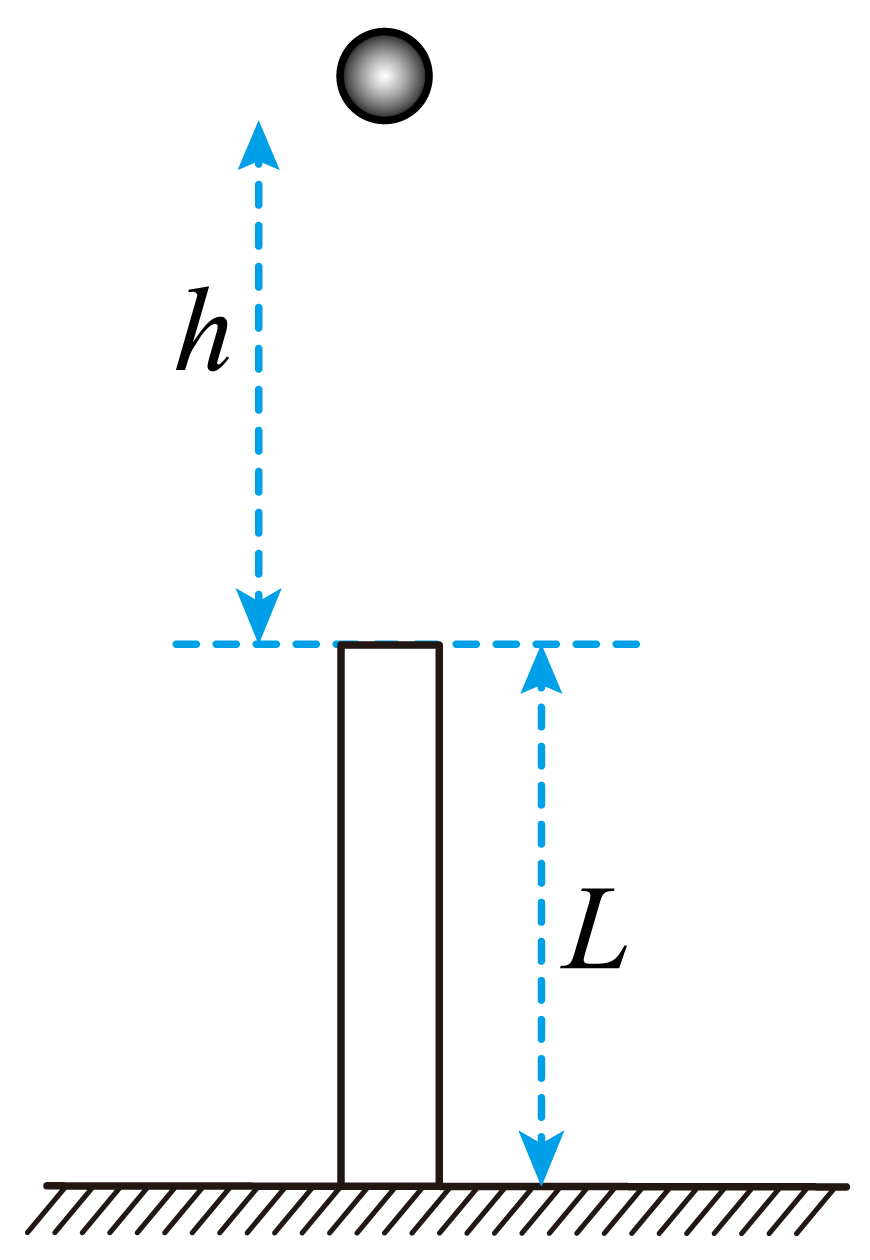(1)若小球在金属管上升阶段穿过管，则v0需要满足什么条件？
(2)若小球在穿过管的过程中，金属管一直处于下降阶段，则v0需要满足什么条件？此时h和L需要满足什么关系？（本题所有结果不必取“=”号）
(1)若小球在金属管上升阶段穿过管，则v0需要满足什么条件？
(2)若小球在穿过管的过程中，金属管一直处于下降阶段，则v0需要满足什么条件？此时h和L需要满足什么关系？（本题所有结果不必取“=”号）
例2：如图所示，AB为空心圆管、C为可视为质点的小球，AB长度为L=2m，AB与C在同一竖直线上，AC之间距离为h=8m。零时刻，AB做自由落体运动，C从地面以初速度v0开始做竖直上抛运动，g取10m/s2。若圆管、小球落地后均不反弹。则下列说法中正确的是（ ）
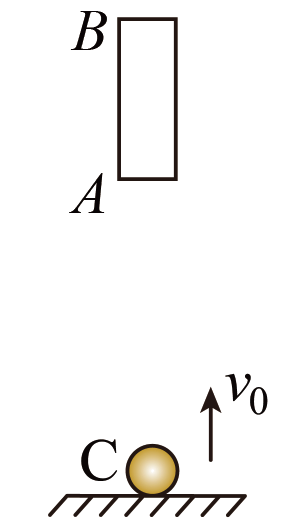
| A．若要使小球在AB落地前从A端穿过AB，则v0应至少为2.5m/s |
| B．若要使小球在上升过程中从A端穿过AB，则v0应至少为10m/s |
| C．若v0=8m/s，则共有三个时刻小球C与圆管A端距离为2m |
| D．若v0=12m/s，则稍降低AC之间距离h后，小球C从A端穿过AB的用时将减少 |