匀变速直线运动的推论一:平均速度和中间时刻速度
一、平均速度、中间时刻速度推论
设物体以初速度,加速度做匀变速直线运动,全程运动时间为,时刻速度为,全程平均速度为。
物体内做匀变速直线运动的位移等效于物体以平均速度做匀速直线运动的位移。
在图像上即两者与t轴围成的面积相等,即,我们由此推出:
若要,必然推出是和的中间值,这个值还对应中间时刻的速度。故:
二、应用情景
平均速度反映的是一段运动过程,瞬时速度反映的是某个位置或者某个时刻。
这个推论的重要之处在于它将平均速度和瞬时速度关联了起来。
它的应用主要有以下两方面:
①不知道具体的运动过程,不知道位移和时间,只知道初末速度或者中间时刻速度,可以利用推论算出整个运动的平均速度
②知道了位移和时间,就可以利用推论计算中间时刻的速度,不需要其他的状态量
1、由瞬时速度算平均速度和位移
用计算位移比位移-时间公式或者要简单很多。
利用平均速度推论,我们可以快速地通过初末速度或中间时刻速度得到平均速度,从而计算位移也会简单很多。
例1:(多选)由静止开始做匀加速直线运动的火车,在第10s末的速度为2m/s,下列说法中正确的是( )
解析:
加速度,B正确
由平均速度推论,C正确
前10s位移,A、D错
例2:汽车从A到B做匀加速直线运动用时12s。已知汽车6s时速度为5m/s,求AB间距离L。
解析:
6s是运动的中间时刻,
| A.前10s内通过的路程为5m | B.速度每秒变化了0.2m/s |
| C.10s内平均速度为1m/s | D.第10s内的位移是2m |
2、由位移、时间算瞬时速度和加速度
对匀变速直线运动来说,加速度是最关键的一个状态量。加速度的计算基于瞬时速度的变化量。
若我们不知道瞬时速度,只知道位移和时间,就可以利用中间时刻速度推论将平均速度转化为瞬时速度。
例1:一个物体以初速度 开始做匀加速直线运动,前4s内的平均速度为
开始做匀加速直线运动,前4s内的平均速度为 ,前8s内的平均速度为
,前8s内的平均速度为 ,则初速度
,则初速度 的大小为( )
的大小为( )
解析:
前4s的中间时刻的速度,
前8s的中间时刻的速度,
加速度
初速度,故选B
| A. | B. | C. | D. |
例2:物体从静止开始做匀加速直线运动,第3s内通过的位移是6m,求物体运动的加速度大小及第3s末的速度大小?
解析:
第3s的平均速度
这也是第3s中间时刻的瞬时速度,
第3s末的速度
例3:物体做匀加速直线运动,已知它在第1个3s内的位移为24m,第2个4s内的位移为64m,求物体的加速度大小。
解析:
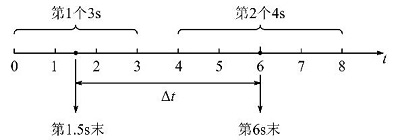 第1个3s内的平均速度等于这段时间的中间时刻时的速度,即
第2个4s内的平均速度等于这段时间的中间时刻时的速度,即
加速度
第1个3s内的平均速度等于这段时间的中间时刻时的速度,即
第2个4s内的平均速度等于这段时间的中间时刻时的速度,即
加速度
 第1个3s内的平均速度等于这段时间的中间时刻时的速度,即
第2个4s内的平均速度等于这段时间的中间时刻时的速度,即
加速度
第1个3s内的平均速度等于这段时间的中间时刻时的速度,即
第2个4s内的平均速度等于这段时间的中间时刻时的速度,即
加速度实验中我们处理纸带数据,要计算瞬时速度,也是利用这个推论。
例4:在“探究小车速度随时间变化的规律”的实验中,电源频率为50Hz。某同学用如图1所示的装置,打出的一条纸带如图2所示,其中ABCDE为计数点,相邻两个计数点之间还有4个点未画出。
则打点计时器打下C点时小车的瞬时速度大小为____________ ;
;
 解析:
相邻两计数点时间间隔。
C点是B、D这段运动的的中间时刻位置,
解析:
相邻两计数点时间间隔。
C点是B、D这段运动的的中间时刻位置,
 解析:
相邻两计数点时间间隔。
C点是B、D这段运动的的中间时刻位置,
解析:
相邻两计数点时间间隔。
C点是B、D这段运动的的中间时刻位置,三、思维拓展
对于匀变速直线运动来说,v-t图像是一条倾斜直线,只要这条直线确定了,这个匀变速直线运动也就唯一确定了。
在数学上,我们确定一条直线的方式有两种,一是通过截距和斜率;二是找到两个不重合的点。
对应在物理中,确定一个匀变速直线运动的方式:
一是知道初速度和加速度;
二是找到两个不相同的时刻和对应的瞬时速度。
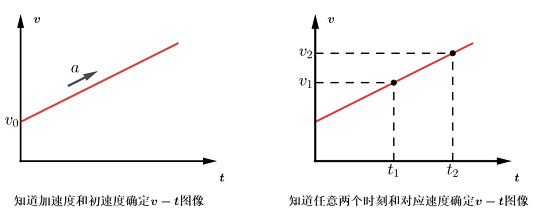 前面所学的基本公式都是基于初速度和加速度,用的是第一种方式。
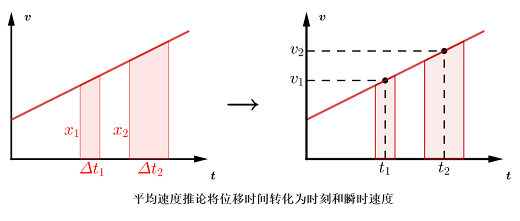
平均速度推论则可以帮我们确定一个时刻的瞬时速度,是用第二种思路解题的的利器。
前面所学的基本公式都是基于初速度和加速度,用的是第一种方式。
平均速度推论则可以帮我们确定一个时刻的瞬时速度,是用第二种思路解题的的利器。
 前面所学的基本公式都是基于初速度和加速度,用的是第一种方式。
平均速度推论则可以帮我们确定一个时刻的瞬时速度,是用第二种思路解题的的利器。
前面所学的基本公式都是基于初速度和加速度,用的是第一种方式。
平均速度推论则可以帮我们确定一个时刻的瞬时速度,是用第二种思路解题的的利器。
