7 Vektorprodukt
Schnapp' dir den Stern, Super Mario!
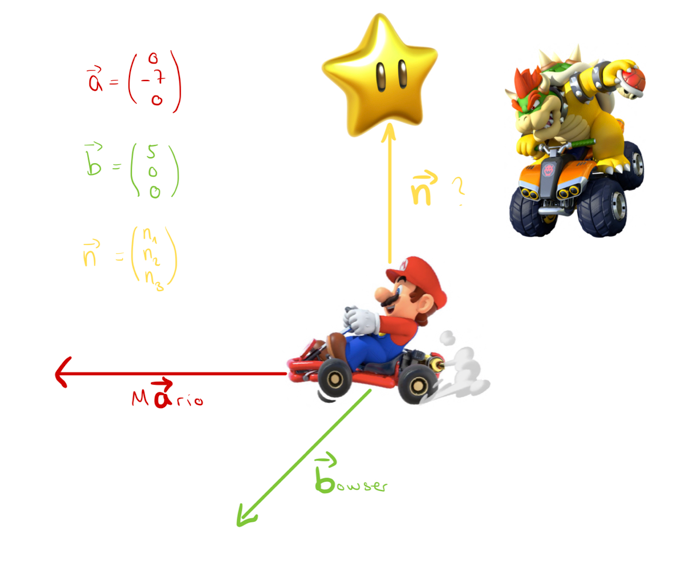
Wir spielen Super Mario Kart. Mario fährt in Richtung der Vektors . Bowsers Wurf trifft ihn und wirkt in Richtung des Vektors . Senkrecht über Mario befindet sich der wertvolle Stern. Wie muss er springen?
Wiederholung
Klar ist, der gesuchte Vektor muss sowohl orthogonal zu als auch sein. Hier hilft uns das Thema der letzten Stunde, das Skalarprodukt. Es gilt also und . Stelle ein entsprechendes Gleichungssystem auf und gib eine allgemein Lösung für an.
Dank vieler Nullen ist das Gleichungssystem hier gar nicht viel Arbeit.
Was ist nun aber, wenn die Vektoren nicht mehr so schön sind. Es wäre durchaus schön nicht immer ein komplettes Gleichungssystem lösen zu müssen. Genau dabei hilft uns das Vektorprodukt - unser heutiges Thema.
Veranschauliche dir den gesuchten Vektor im GeoGebra-Applet ("vor"-Button klicken.)
Sieh dir jetzt das folgende Video an um zu lernen, wie man diesen Vektor algebraisch finden kann.
Übertrage nun den Hefteintrag und sieh dir das Erklärvideo dazu an.
Hefteintrag: 7 Vektorprodukt
Erklärvideo
Anmerkungen:
- Wegen der Sprechweise "a kreuz b" wird das Vektorprodukt auch als Kreuzprodukt bezeichnet.
- Das Ergebnis des Skalarprodukts ist ein Skalar (eine Zahl), das des Vektorprodukts ein Vektor.
Das üben wir gleich mal mit der folgenden Basisaufgabe.
Buch S. 113

Lösung
Doch das Vektorprodukt kann noch viel mehr als "nur" orthogonale Vektoren zu finden. Mit seiner Hilfe kann man sehr einfach Flächen- und Volumenberechnungen durchführen.
Wir starten mit den Flächenberechnungen. Sieh dir dazu zunächst folgendes Applet an.
Wir haben oben bereits gelernt, dass und ein Parallelogramm aufspannen. Dieses hat die Fläche .
ist die Höhe des Parallelogramms. Sie steht senkrecht auf .
Deshalb können wir sagen
Also gilt auch, dass .
Merke dir diese Beziehung und sieh dir das nächste Video an.
Der Betrag des Vektorprodukt macht es uns also super einfach den Flächeninhalt eines Parallelogramms im Raum zu berechnen.
Übertrage dazu folgenden Hefteintrag:

Das üben wir gleich mal. Löse zwei von drei Teilaufgaben.
Tipp: Ein Dreieck ist ein halbes Parallelogramm.
Buch S. 113

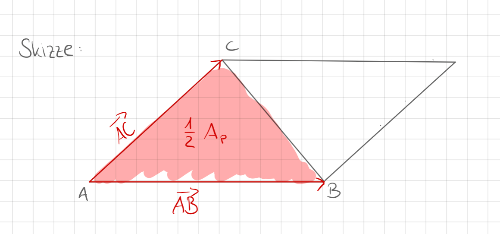
Lösung
Weiter geht's mit der nächsten Übung. Hier sollst du einen bestimmten Vektor ermitteln, der zu zwei gegebenen Vektoren orthogonal ist.
Tipp: Vergiss nicht, dass alle Vielfachen des Vektorprodukts orthogonal zu den gegebenen Vektoren sind.
Buch S. 114

HAUSAUFGABE:
Bearbeite die folgenden Aufgaben.

Tipps zur Hausaufgabe:
1. analog zu Aufgabe 2, reines Formeleinsetzen
2. analog zu Aufgabe 12
3.a) analog zu Aufgabe 3
b) Formel umstellen
freiwillige Zusatzaufgaben:
Die Rechengesetze für das Skalarprodukt lassen sich leicht nachrechnen. Nutze einfach allgemeine Vektoren, wie um die Gesetze zu beweisen. Gerne kannst du mir deine Lösung zur Korrektur im Chat schicken.
Buch S. 114

