GeoGebra

1.3 continuidad de funciones

Autor:Pablo Pardo

Tipos de continuidad

  • continuidad en un punto
Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto. La continuidad de f en x=a implica que se cumplan estas tres condiciones: a.- Existe el límite de la función f(x) en x=a. b.- La función está definida en x=a, es decir, existe f(a). c.- Los dos valores anteriores coinciden.
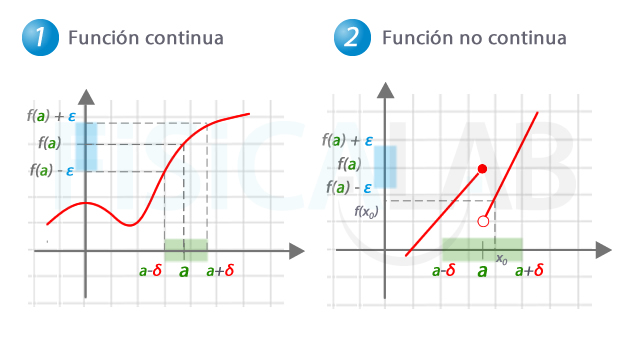
Image
  • continuidad en un intervalo abierto
Una función es continua en un intervalo abierto o unión de intervalos abiertos si es continua en cada punto de ese conjunto. Decimos que una función es continua en un intervalo abierto (a,b) cuando es continua en todos los puntos pertenecientes a dicho intervalo.
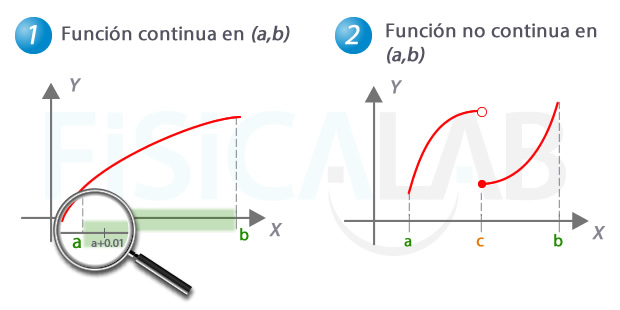
Image
  • continuidad en un intervalo cerrado
Decimos que una función es continua en un intervalo cerrado [a,b] cuando: f(x) es continua en el intervalo abierto (a,b). Esto cubre todos los puntos del intervalo salvo los extremos limx→a+f(x)=f(a) y limx→a−f(x)=f(b). Esto contempla la continuidad por la derecha de a y la continuidad por la izquierda de b respectivamente
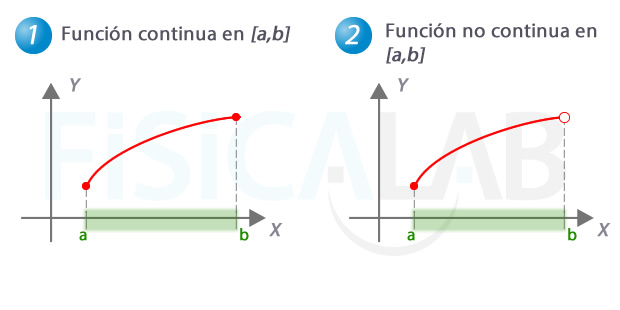
Image

PROCEDIMIENTO PARA DETERMINAR LA CONTINUIDAD

FUNCIONES CONTINUAS Para algunas familias de funciones es posible conocer su continuidad basándose en los siguientes criterios generales:
  • Las funciones polinómicas son continuas en todo el conjunto de los números reales.
  • Las funciones racionales obtenidas como cociente de dos polinomios son continuas en todos los puntos del conjunto R, salvo en aquellos en los que se anula el denominador.
  • Las funciones potenciales, exponenciales y logarítmicas son continuas en todo su dominio de definición.
  • Las funciones trigonométricas seno y coseno son continuas en todo el conjunto de los números reales 
PROPIEDADES DE LAS FUNCIONES CONTIUNAS Dadas dos funciones f(x) y g(x) continuas en un punto o en un intervalo, se cumple entonces que:
  • La suma y la resta de ambas es una función continua en ese punto o intervalo.
  • El producto de las dos funciones es una función continua en ese punto o intervalo.
  • El cociente entre ambas funciones es una función continua en ese punto o intervalo salvo en aquellos en los que el denominador se anula.
  • Si f(x) es continua en a y g(x) es continua en f(a), entonces la composición de funciones (g ° f) (x) es también continua en a.
DISCONTINUIDADES EVITABLES Toda función que en un punto dado no cumple alguna de las condiciones necesarias para la continuidad se denomina discontinua. Cuando la discontinuidad se debe al hecho de que existe el límite de la función en el punto, pero la función no está definida para el mismo, se habla de discontinuidad evitable. Para obtener una nueva función que sea continua también en el punto de discontinuidad evitable, se procede del modo siguiente:
  • Se calcula el valor del límite de la función en el punto a.
  • Se añade el punto a al dominio de definición de la función, y se le asigna el valor
DISCONTINUIDADES NO EVITABLES Existen otros tipos de discontinuidades que no pueden resolverse, por lo que se llaman discontinuidades no evitables. Estas discontinuidades se clasifican en:
  • Discontinuidades de salto: cuando existen ambos límites laterales (por la derecha y por la izquierda), pero no coinciden.
  • Discontinuidades asintóticas: cuando el límite es infinito.
  • Discontinuidades por el dominio de definición: cuando existe el límite y la función está definida en el punto, pero ambos valores no coinciden.
En sentido genérico, se llama discontinuidad de segunda especie a la que tiene lugar cuando uno de los límites laterales es finito y el otro es infinito o no existe.

Preguntas generales

Que es una función definida por partes? Que es el limite de una función? Que tipos de continuidad hay ? Que es una función continua? Que es una función discontinua?

Nuevos recursos

Descubrir recursos

Descubre temas