SRT.2 Similarity Notes 2
SRT.2 I can use similarity conditions, congruent angle pairs and proportional sides, to determine if two figures are similar.
SRT.2 Conditions of Similarity: 1. Congruent Angle Pairs 2. Proportional Sides

Similarity Conditions: Congruent Angle Pairs
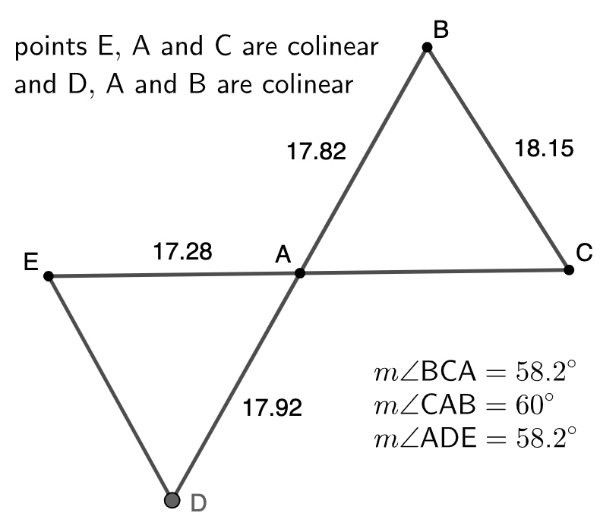
Using Similarity Conditions
Do you think the two triangles are similar? Explain why or why not.
Congruent Angle Pairs & Proportional Sides
If the triangles are similar, use proportional sides to determine the length of side AC
Congruent Angle Pairs & Proportional Sides
If the triangles are similar, use proportional sides to determine the length of side ED
Proportional Sides
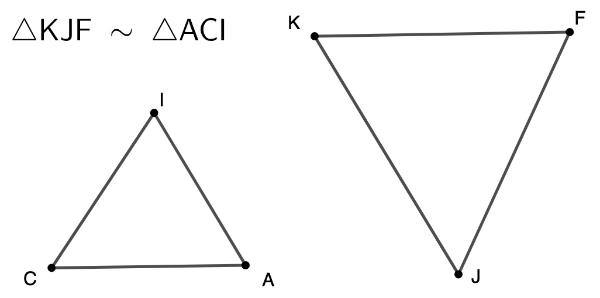
Proportional Sides
Write three proportions to represent which sides are proportional to which. Express your three proportions like this: with the three sides of one triangle in the numerators positions and the proportional three sides of the other triangle in the denominator positions.
the Cross-Produce Rule
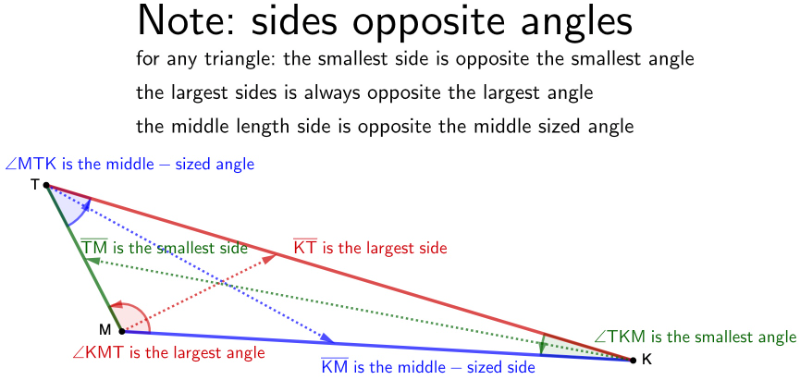
Triangles Largest side opposite Largest Angle, Smallest Side opposite Smallest Angle
Similarity Condition: Proportional Sides
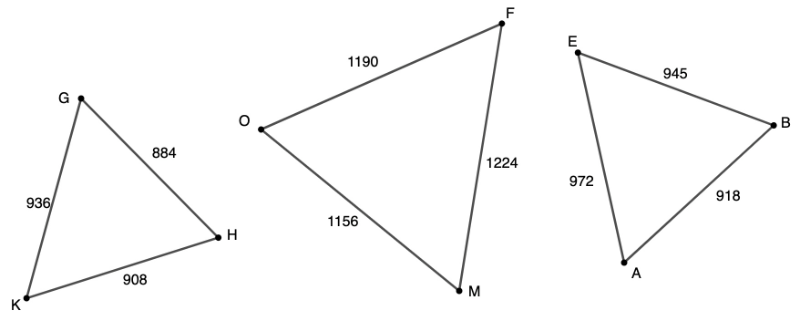
Testing triangles for similarity: proportional sides
If any two triangle are similar, then you should be able to write THREE proportions, like this Test each pair of triangle, by testing the proportions of each pair. Since you will be testing 3 pairs of triangle, you will need to test 9 proportional statements (three for each pair) Which of the triangles above are similar?