Projeção de um cubo em um plano
Problema
"Seja um cubo de borda uma unidade e p sua projeção ortogonal sobre um plano". Qual é o valor máximo de p(C)?"
Observação
O problema acima aparece na edição 180 da revista "tangente" (janeiro-fevereiro de 2018), cujo tema é "Espionagem: matemática, em toda parte!".
Jean-Michel Sarlat dá uma solução:
http://ww2.ac-poitiers.fr/math/IMG/pdf/cg97c.pdf
Procedimento
A ilustração da solução deste problema é feita considerando um número , onde , um altura e os pontos , e com as coordenadas
, , e .
- A partir desses pontos determinamos os pontos , , e com retas perpendiculares ao plano que passa por , e e cuja distância a esse plano seja. Assim, temos o cubo
- Determinamos a projeção de cada ponto no plano . A projeção dos pontos e está no interior do polígono formado pelas projeções dos pontos , , , , e .
- Consideramos o triângulo para determinar o triângulo equilátero de área máxima no plano . O baricentro desse triângulo é o ponto com coordenadas .
- As coorodenadas das projeções dos pontos e no plano coincidem comas coordenadas do ponto quando .
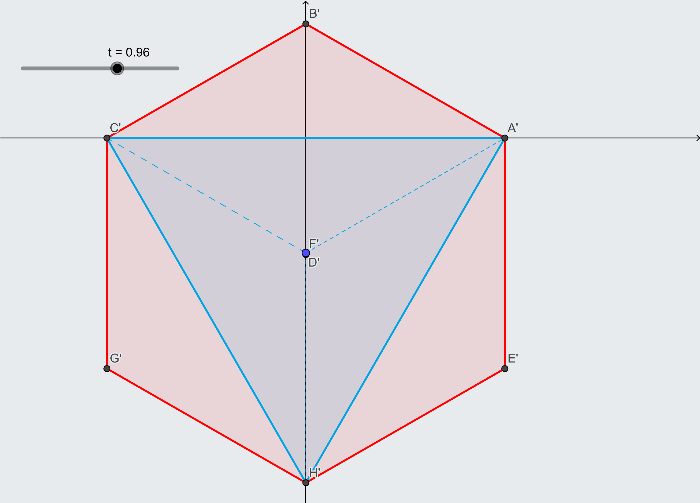
A projeção máxima do cubo é um hexâgono regular
Discussão
A área máxima da projeção do cubo no plano é e essa solução não depende da altura .
Atividade
Verifique que a solução é obtida quando