Outline
Currents and magnetic fields of stator of 1PH induct. motors
This GeoGebra book illustrates the currents through the main and auxiliary stator windings, as well as the magnetic flux densities produced by those currents, in a four-total-magnetic-poles single-phase AC induction motor. This book is a follow-up of this answer in Quora I wrote: https://www.quora.com/Since-a-capacitor-is-used-in-single-phase-induction-motors-to-make-a-90-phase-shift-why-is-the-auxiliary-winding-placed-perpendicular-to-the-main-winding-Or-why-dont-we-just-place-the-windings-perpendicular-without/answer/Alejandro-Nava-2.
You're able to adjust the phase angle between the stator windings currents, such that you can mimic the different types of single-phase AC induction motors: resistor-start or split-phase motor, capacitor-start motor, capacitor-run or permanent split-capacitor motor, and double-capacitor or capacitor-start capacitor-run motor. The shaded-pole motor is not studied in this GeoGebra book.
I use the term magnetic flux density to refer to the B-field because the term magnetic field is ambiguous (it can also refer to the H-field, called the magnetic field intensity). For further details on this terminology, read: https://en.wikipedia.org/wiki/Magnetic_field#Description.
The book consists of four apps, each illustrating different quantities, which are, in order:
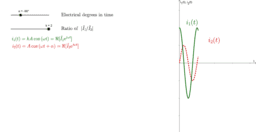
- Real instantaneous values of stator currents.
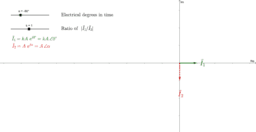
- Phasors of stator currents.
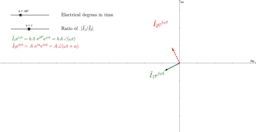
- Sinors or complex instantaneous values of stator currents.
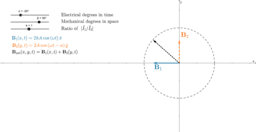
- Real instantaneous values of stator magnetic flux densities.
- The term real instantaneous value is a synonym of instantaneous value, which refers to the representation of signals (currents, voltages, magnetic fields, electric fields, etc.) as instantaneous quantities, for example "i(t)", "v(t)", "E(x,y,z,t)", "B(x,y,z,t)", etc. They are real functions of real variable(s): always a time variable, and sometimes also one, two or three spatial variables. If the signal is the real instantaneous current through or voltage across a lumped device (such as resistors, inductors, capacitors, diodes, voltage and current sources), then the real instantaneous value is a real function of one real variable: a time variable. If the signal is the real instantaneous current through or voltage across a distributed device (such as transmission lines), then the real instantaneous value is a real function of two real variables: a time variable and one spatial variable. If the signal is an electric or magnetic field propagating in a medium (such as air or vacuum), then the real instantaneous value is a real function function of four real variables: a time variable and three spatial variables.
- A phasor is a complex quantity always independent of time that represents the magnitude (either the amplitude/peak value/maximum value or the RMS/effective value) and the phase angle but not the frequency of a real sinusoidal signal. If the signal is the real instantaneous current through or voltage across a lumped device, then the phasor is a complex constant. If the signal is the real instantaneous current through or voltage across a distributed device, then the phasor is a complex function of one real variable: one spatial variable. If the signal is an electric or magnetic field propagating in a medium, then the phasor is a complex function of three real variables: three spatial variables.
- The term sinor is used by Charles Alexander and Matthew Sadiku in their textbook Fundamentals of Electric Circuits (5th edition) on page 379 (section 9.3, titled Phasors). It refers to the product of a phasor times e^(jωt). They are always complex functions of real variable(s): always a time variable, and sometimes also one, two or three spatial variables. It is also called the complex instantaneous value by William Hayt and John Buck in their textbook Engineering Electromagnetics (8th edition) on page 312 (section 10.5, titled Complex Analysis of Sinusoidal Waves), in the context of transmission lines. Since the sinor is also called the complex instantaneous value, to distinguish it from the instantaneous value, William and John call the later as real instantaneous values. If the signal is the real instantaneous current through or voltage across a lumped device, then the sinor or complex instantaneous value is a complex function of one real variable: a time variable. If the signal is the real instantaneous current through or voltage across a distributed device, then the sinor or complex instantaneous value is a complex function of two real variables: a time variable and one spatial variable. If the signal is an electric or magnetic field propagating in a medium, then the sinor or complex instantaneous value is a complex function of four real variables: a time variable and three spatial variables.
- i_1(t) is the instantaneous current of the auxiliary winding (the winding that would have the capacitor).
- i_2(t) is the instantaneous current of the main winding (the winding that wouldn't have the capacitor).
- The angle "α" is the angle by which "i_2(t)" leads in time "i_1(t)", or equivalently, it's the angle by which "i_1(t)" lags in time "i_2(t)". Therefore, "-α" is the angle by which "i_2(t)" lags in time "i_1(t)", or equivalently, it's the angle by which "i_1(t)" leads in time "i_2(t)". Thus, to make the auxiliary winding current lead the main winding current by +90° in time, adjust "α" to "-90°".
- The angle "β" is the angle that the main winding and the auxiliary winding make in space. Thus, to make the main winding be in the same spatial axis as the auxiliary winding, adjust "β" to "0°". To make the main winding be perpendicular to the auxiliary winding, adjust "β" to "90°".
- The factor "k" is the magnitude of the ratio of the phasor of the auxiliary winding current to the phasor of the main winding current. Thus, to make the currents (and thus their corresponding individual magnetic fields) have the same amplitude, adjust "k" to "1". If "k > 1", the current of the auxiliary winding ("i_1(t)") has greater amplitude than the current of the main winding ("i_2(t)"). If "0 < k < 1", the current of the auxiliary winding ("i_1(t)") has smaller amplitude than the current of the main winding ("i_2(t)").
- "α ≠ 0°".
- "β ≠ 0°".
- "k = 1", that is, the individual magnetic fields have the same amplitude, which would mean their respective currents also have the same amplitude.
- "|α| + |β| = 180°", where "α" and "β" are measured between -180° and 180°.
- "α ≠ 0°" and "β ≠ 0°" and "|α| + |β| = 180°" and "k ≠ 1".
- "α ≠ 0°" and "β ≠ 0°" and "k = 1" and "|α| + |β| ≠ 180°".
- "β = 0°" and "α ≠ ±180°".
- "α = 0°" and "β ≠ ±180°".
- "β = ±180°" and "α ≠ 0°".
- "α = ±180°" and "β ≠ 0°".
- "β = 0°" and "α = ±180°".
- "α = 0°" and "β = ±180°".