Binomialverteilung

E1: Schlüsseldienst
Du möchtest einen Schlüssel nachmachen lassen, der die Truhe öffnet. Verwende das Applet (unten), um die Parameter des Schlüssels zu finden.
E2: Zweites Schloss
Ein weiteres Schloss hängt an der Truhe. 1. Entscheide nun, ob du zuerst n oder zuerst p variieren würdest, damit du möglichst schnell zum Ziel gelangst. 2. Entscheide welcher Parameter sich zum letzten Schloss geändert hat.
P3: CAS
1. Vergleicht die Reihenfolge, wie ihr die Parameter am besten bestimmen würdet.
2. Lasst euch nun das Histogramm im CAS anzeigen:
P4: Vergleicht die Ausgabe mit dem folgenden Bild
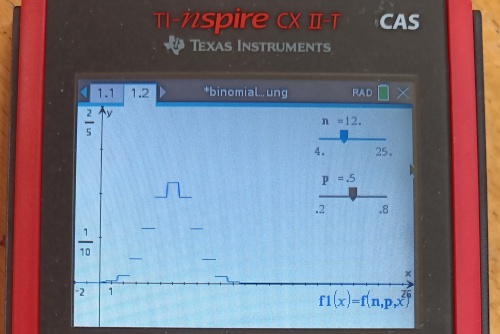
Expert5: Glücksräder des Flaschengeists
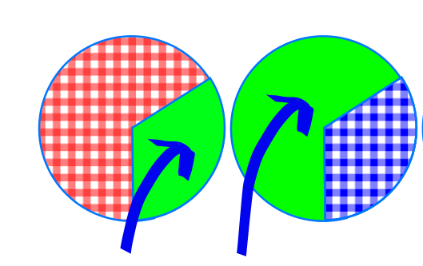
Drittes Schloss
Als du das zweite Schloss der Truhe öffnest, kommt aus ihm ein Flaschengeist. Er gibt jedem von euch einen Schlüssel, insgesamt 4 unterschiedliche. Er sagt: Der Schlüssel, der die Truhe öffnet, kann keinem der folgenden Zufallsexperimenten zugeordnet werden: A: “21-mal das zweite Glücksrad drehen” B: “n-mal das erste Glücksrad drehen, dabei ist n fest, ist aber nicht 21” C: “21-mal das zweite Glücksrad drehen” 1. Verwendet die Schieberegler des CAS, um den euch ausgeteilten Schlüssel als Binomialverteilung zu veranschaulichen. 2. Lest die Parameter ab. 3. Entscheidet, wie oft man (egal welches Glücksrad) drehen muss, um euer n zu erhalten. 4. Vergleicht gemeinsam die Glücksräder. Entscheidet euch für das Glücksrad, um euer p zu erhalten.
Anwender6:
Findet euch in Gruppen zusammen, die alle Schlüsselsorten auf einem ihrem CAS veranschaulichen. Welcher Schlüssel passt zu keinem Zufallsexperiment? Öffnet das Schloss