Secciones cónicas
Se denominan SECCIÓN CÓNICA a la curva formada por la intersección de plano con un cono.
¿RECUERDAS las ecuaciones de rectas y planos en el espacio?. Si no las recuerdas repásalas.
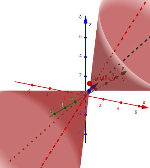
CONO
Un CONO es aquel que se puede generar al girar una recta s con respecto a otra no paralela r (EJE DE ROTACIÓN), y cuyo VÉRTICE es .
Si es el vector director de r tal que y .
Un punto pertenece al CONO si cumple:
Que equivale a la ecuación:
Desarrollando, esta expresión y teniendo en cuenta que , su ecuación implícita será:
CONO: Selecciona las casillas de control y escribe los datos adecuados.
Observación:
Si y , dividiendo por , queda la ecuación:
SECCIONES CÓNICAS
Para entender mejor las secciones cónicas, veamos una cónica particular:
Tomemos el cono de vértice , el vector director del eje del cono , siendo el ángulo entre el eje del cono y el plano .
La intersección del cono y del plano vendrá dada por la ecuaciones:
Resultando la ecuación de la CÓNICA:
Que denominando:
La ecuación de la cónica queda como:
Cónica particular
OBSERVACIONES
Como y , A>0, y por tanto:
1.- Si la cónica es una ELIPSE.
2.- Si la cónica es una PARÁBOLA.
3.-Si la cónica es una HIPÉRBOLA.
En el caso particular de que , tenemos una CÓNICA DEGENERADA, cuyas posibles soluciones serían:
1.- Si La única solución es el punto .
2.- Si La solución es la recta que contiene al eje OY.
3.- Si La solución son dos rectas no paralelas que pasan por el origen de coordenadas y que están sobre el plano .

