Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Complex numbers AAHL 1.11,1.12

Tekijä:Cliff Packman
Complex numbers複素数복소수复数
Real part実部실부实部
Imaginary part虚部허부虚部
Modulus絶対値모듈러스模
Argand diagramアルガン図아르간 도표阿尔冈图
Complex conjugates共役複素数복소 공액共轭复数
Imaginary unit (i)虚数単位허수 단위(i)虚数单位
Geometric transformations幾何変換기하학적 변환几何变换
Image

Inquiry questions

Factual Inquiry Questions
  • What defines a complex number?
  • How is the real part of a complex number represented on the complex plane?
  • What is the result of adding two complex numbers algebraically?
  • Can you list the steps to multiply two complex numbers?
  • How do we find the modulus of a complex number?
Conceptual Inquiry Questions
  • How does the concept of complex conjugates aid in the division of complex numbers?
  • In what way does multiplying a complex number by i (the imaginary unit) affect its position on the Argand diagram?
  • What is the significance of the angle a complex number makes with the positive real axis, and how is it related to the number’s multiplication and division?
  • Can you explain the relationship between the operations of addition, subtraction, multiplication, and division of complex numbers and the geometric transformations on the complex plane?
Debatable Inquiry Questions
  • Is there a situation in which the division of complex numbers would give an unexpected result, perhaps not conforming to the usual patterns observed on the complex plane?
  • Can the behavior of complex numbers under various operations be considered analogous to physical movements or transformations in space? How might this analogy break down?
  • To what extent do the operations on complex numbers challenge our traditional understanding of dimensions in mathematics?
  • Are complex numbers truly "complex" when their behavior is quite predictable and follows geometric patterns, or is the term misleading?
  • How might the concept of complex numbers be extended or modified to better model phenomena in advanced physics or other sciences?

Introduction

Complex numbers are written in the form , where: - is the real part - is the imaginary part - i is the imaginary unit with the property that For example, has and

Checking your understanding

Given the complex number , where What are the real part and the imaginary part of the complex number ?

Valitse ne, jotka kelpaavat
  • A
  • B
  • C
  • D
  • E
Tarkista vastaus (3)

Consider the complex number defined by Determine the real part and the imaginary part of the complex number .

Valitse ne, jotka kelpaavat
  • A
  • B
  • C
  • D
  • E
Tarkista vastaus (3)

Geometric approach

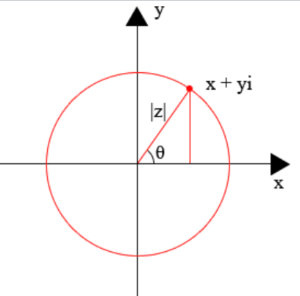
Real numbers can be visualized on a number line. Each point on the line represents one real number. In a similar way, complex numbers can be represented in a two-dimensional coordinate plane, where the horizontal axis represents the real part of the number, and the vertical axis represents the imaginary part of the number. Each complex number , , is represented by a point in the plane and the coordinates are the real and imaginary parts of the complex number itself. Purely real numbers lie on the x-axis, and purely imaginary numbers lie on the y-axis.

The Argand diagram

The Argand diagram
Geometric representation of the complex-valued point z = x + yi in the complex plane. The distance along the line from the origin to the point z = x + yi is the modulus or absolute value of z. The angle θ is the argument of z.

Part 1 - Experimenting with arithmetic with complex numbers

In this section we are exploring what the results of the operations of addition, subtraction, multiplication and division have on the numbers geometrically. We will look at much of this in more depth and for now it's just to see what we can see.

Experiment with adding different complex numbers

Consider these discussion questions  How does adding a real number to a complex number affect its position on the complex plane? What is the result of adding two complex numbers geometrically in terms of movement along the axes? Can you predict the sum of a real and an imaginary number by their positions on the complex plane? What patterns emerge when adding complex numbers along the same line in the complex plane?

Adding complex numbers

Subtracting complex numbers

Consider these discussion questions How does the result of subtracting from , as shown by , reflect their relative positions on the complex plane? If and were points on a vector field, what would the vector represented by indicate? How can we interpret the subtraction of two complex numbers in terms of movement along the real and imaginary axes? What would be the geometric interpretation if were subtracted from , instead of from ? If is fixed and varies, how does map out a path on the complex plane?

Experimenting with dividing complex numbers

Consider these discussion questions How does the division of complex numbers alter their position on the complex plane? What happens to the magnitude and direction of a complex number when it is divided by another complex number? How can you use the concept of conjugates to simplify the division of complex numbers? Can you predict the quotient of two complex numbers by examining their positions on the complex plane? How does the division of a complex number by a real number compare to division by an imaginary number on the complex plane? If and are both on a of the form , what do you notice?

Dividing complex numbers

Multiplying complex numbers

Consider these discussion questions  How does the multiplication of a complex number by a real number affect its position on the complex plane? What type of number does multiplying two purely imaginary numbers together give? What geometric transformation occurs when multiplying a complex number by i? Can you predict the product of a complex number with a purely imaginary number based on their initial positions? What is the result of multiplying two complex numbers that are each other's conjugates?

Multiplying complex numbers

Powers of a complex number

Consider these discussion questions What happens to the magnitude of a complex number when it is raised to higher powers? How does the angle of a complex number with the positive real axis change with successive powers? Can you describe the pattern formed by the powers of a complex number on the complex plane? What does the image suggest about the convergence or divergence of the powers of the complex number? How would changing the initial complex number affect the pattern of its powers on the complex plane? Can you predict the n-th power of a given complex number without actual calculation, using its position on the complex plane? Take a complex number with a magnitude of 1. For example, or or what do you notice about powers of numbers of this form?

Part 2 - Arithmetic with complex numbers algebraically

Here we will explore how to add, subtract, multiply and divide complex numbers algebraically.

Part 2 - Arithmetic with complex numbers algebraically

Here we will explore how to add, subtract, multiply and divide complex numbers algebraically.

Experiment with your own examples to check that you can perform the four operations manually and with your GDC

Part 3 - Checking your understanding

Check your understanding with these exam style questions
Practice questions 1-6 Section A - style short response style questions 7-19 Challenge questions 20-21

[MAA 1.11-1.12] COMPLEX NUMBERS (CARTESIAN FORM)

[MAA 1.11-1.12] COMPLEX NUMBERS (CARTESIAN FORM).pdf

[MAA 1.11-1.12] COMPLEX NUMBERS (CARTESIAN FORM).pdf

[MAA 1.11-1.12] COMPLEX NUMBERS (CARTESIAN FORM)_solutions

[MAA 1.11-1.12] COMPLEX NUMBERS (CARTESIAN FORM)_solutions.pdf

[MAA 1.11-1.12] COMPLEX NUMBERS (CARTESIAN FORM)_solutions.pdf

Part 4 - Optional extension challenge

Part 4 - Optional extension challenge

Step 1: Multiplying a complex number by it's complex conjugate, will always give a real ouput. Can you algebraically prove this?

Step 1: Multiplying a complex number by it's complex conjugate, will always give a real ouput. Can you algebraically prove this?

But what if we wanted a different real number, n.

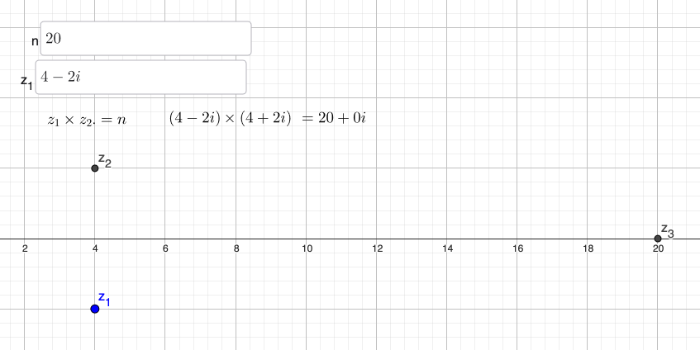
But what if we wanted a different real number, n.
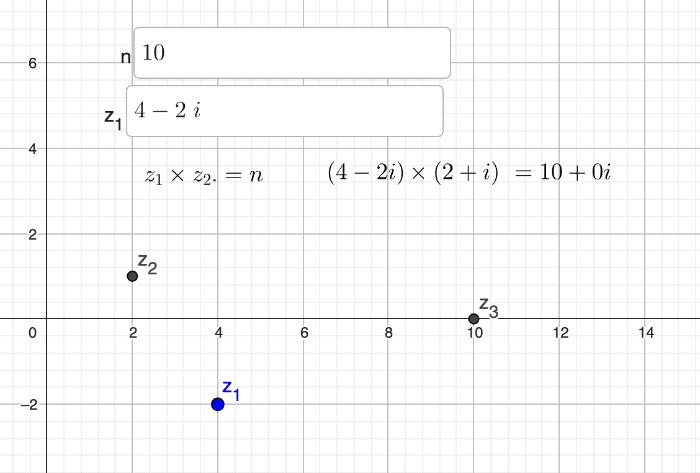
Can you find the required for any given and ?

Lesson Plan - Navigating Complex Numbers

Navigating Complex Numbers.pdf

Navigating Complex Numbers.pdf

Complex numbers - Intuition pump (thought experiments and analogies)

Complex numbers AAHL 1.pdf

Complex numbers AAHL 1.pdf

Uusia resursseja

Löydä Materiaaleista

Löydä aiheita