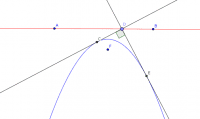
Skica
放物線の基本定理
放物線とその準線には面白い性質がある。
そこで、放物線に外接する三角形を作図してみる。
すると、この三角形の心と焦点や極との間に面白い性質が見つかってくる。
それらの発見を一つずつシートにしていたら、そこには何かつながりがありそうだと感じる。
そこでこれらのシートをブックで一つにまとめてみる。
だんだんとそれらのシートの間の関係が見えてくる。
編集とはこういう作業。
今回は性質を見つけるだけではなく、証明も試みてみた。
でも、「垂心が準線上にある定理」は証明するのに一か月以上かかってしまった。(「極線が重心を通る定理」も一か月以上)
後から振り返ると、「垂心の性質」と「外接する三角形の外接円は焦点を通る」から自然に導くことができるのだけど、
あれやこれやとさ迷っていた時には道が見えなかった。
だからこそ証明できた時はとても嬉しかった。
そして、なぜ証明ができたのかをたどってみたら、それは山登りのような景色だった。
これらは逆に考えると、三角形に内接する円錐曲線の特別な場合ということが言える。
その関係も面白そう。