Función logaritmo natural
Introducción
El logaritmo natural de un número x es el exponente al que debe ser elevado el número e para obtener x.
Por ejemplo el logaritmo natural de 20.0855.. es 3 ya que e3 = 20.0855…
El logaritmo de e es 1, por lo tanto e1=e.
La función logaritmo natural, ln, se define por:
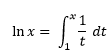 para toda x > 0
La función logaritmo natural es continua y creciente en todo su dominio.
Propiedades los logaritmos naturales
para toda x > 0
La función logaritmo natural es continua y creciente en todo su dominio.
Propiedades los logaritmos naturales
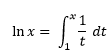 para toda x > 0
La función logaritmo natural es continua y creciente en todo su dominio.
Propiedades los logaritmos naturales
para toda x > 0
La función logaritmo natural es continua y creciente en todo su dominio.
Propiedades los logaritmos naturales- ln 1 = 0
- ln e = 1
- ln en = n
- ln (x · y) = ln (x) + ln (y)
- ln (x / y) = ln (x) − ln (y)
- ln xn = n ln (x)
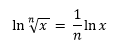
- ln 2 = .6931…
- ln 1/2 = -.6931…
- ln e-3 = -3
- ln e2/3 =.666…
- ln 1 = 0
¿Hay logaritmos naturales negativos?
¿Cuál es el punto coordenado por el cual pasan todas las coordenadas logarítmicas?
¿Qué es un logaritmo y para qué sirve?
![[url=https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/graphing-logarithmic-functions]Graficados[/url]](https://www.geogebra.org/resource/mt3atsq2/R1fzS4JSPhoIfBet/material-mt3atsq2.gif)