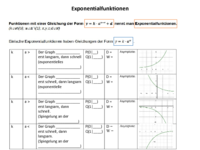
Eigenschaften der Exponentialfunktion 1
1.
b) Finde (näherungsweise) die Funktionsgleichung zu dem Graphen E aus dem Bild zu Aufgabe 2. (siehe unten)
2.
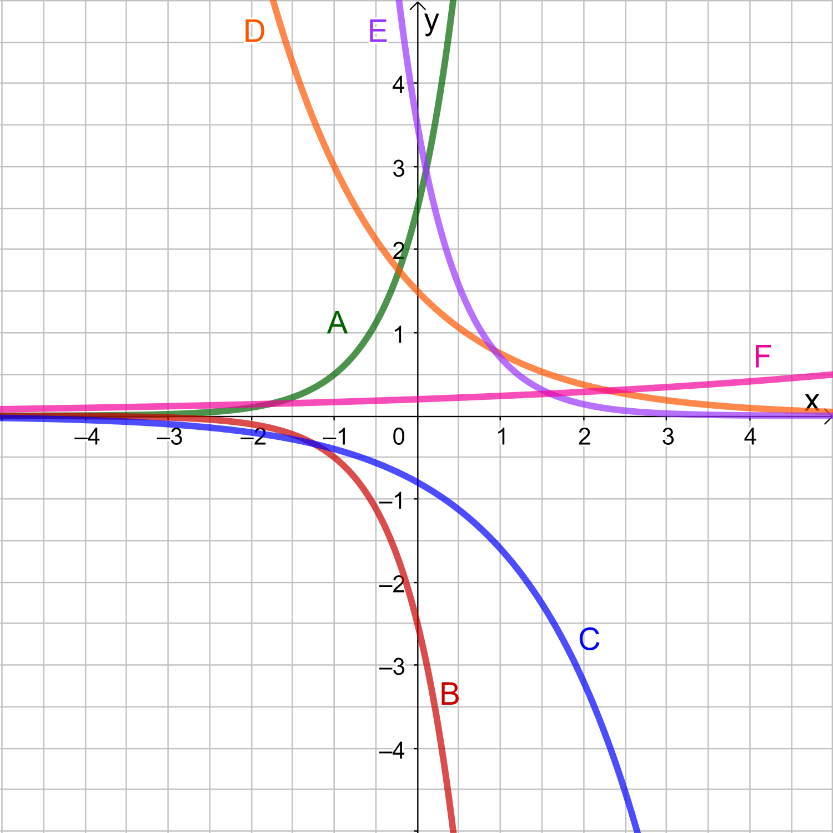
Ordne der Funktionsgleichung den entsprechenden Graph (A, B, C, D oder F) zu.
Ordne der Funktionsgleichung den entsprechenden Graph (A, B, C, D oder F) zu.
Ordne der Funktionsgleichung den entsprechenden Graph (A, B, C, D oder F) zu.
Ordne der Funktionsgleichung den entsprechenden Graph (A, B, C, D oder F) zu.
Ordne der Funktionsgleichung den entsprechenden Graph (A, B, C, D oder F) zu.
3.
Richtig oder falsch? Der Graph der Exponentialfunktion f: schneidet die y-Achse im Punkt P(0|4).
Der Graph der Exponentialfunktion f: schneidet die y-Achse im Punkt P(0|4).
Der Graph der Exponentialfunktion f: steigt.
Die Gerade g mit y=0 (x-Achse) ist Asymptote an den Graph der Exponentialfunktion f: .