RELAÇÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO QUALQUER
PROPOSTAS:
O triângulo é o mais simples dos polígonos, mas é de suma importância, pois é o único polígono que goza da propriedade de rigidez, indeformável, mantem o equilíbrio, é considerado como unidade na decomposição dos polígonos em triângulos. Entre as diversas classificações de triângulos destacam-se o triângulo retângulo com diferentes aplicações no ensino e aprendizagem da matemática tanto na geometria plana como espacial euclidiana. No triângulo retângulo os lados recebem nomes específicos; lado maior, oposto ao ângulo reto denomina-se hipotenusa, os dois outros lados, adjacentes ao ângulo reto são designados de catetos.
PRETENSÕES:
Pretende-se focalizar as relações (ou razões) trigonométricas no triângulo retângulo qualquer, relacionando três elementos [conforme aponta o prefixo tri (três]): cada um dos ângulos agudos envolvendo com os lados, utilizando a semelhança de triângulos, com uma perspectiva dinâmica, desafiadora, construtiva e prática.
ALVO:
Educandos da educação básica: 9º ano do ensino fundamental e do ensino médio.
PRESCRIÇÕES:
A trigonometria retangular tem uma vasta aplicação na matemática, física, agrimensura, astronomia, engenharia, navegação, gerações e construções de instrumentos de precisão e utensílios...
RELAÇÕES (RAZÕES):
1 ª - Seno de : sen = (Cateto oposto a ) / (Hipotenusa);
2 ª - Cosseno de : cos =(Cateto adjacente a ) / (Hipotenusa);
3 ª - Tangente de : tg == (Cateto oposto a ) /(Cateto adjacente a );
4 ª –Cotangente de : cotg =(Cateto adjacente a ) / (Cateto oposto a );
5 ª - Seno de = sen = (Cateto oposto a ) / (Hipotenusa);
6 ª - Cosseno de : cos = =(Cateto adjacente a ) / (Hipotenusa);
7 ª -Tangente de : tg = (Cateto oposto a ) /(Cateto adjacente a );
8 ª - Cotangente de : cotg ==(Cateto adjacente a ) / (Cateto oposto a );
QUESTÃO 1
Fazer controle deslizante (seletor): = 45º Þ = , em seguida: ativar a caixa e Relações com b(Caixa de Exibir/ Esconder Objetos), animar manualmente o controle deslizante (seletor): n, verificar o que aconteceu com as medidas do seno e do cosseno?
QUESTÃO 2
Ainda comseleção da Questão 1 ativa, os triângulos formados são denominados de?
QUESTÃO 3
Ativar as duas (Caixa de Exibir/ Esconder Objetos), respectivamente, e Relações com e f Relação com . Mediante a observação das oito razões entre os dois ângulos agudos e os lados sen é igual?
QUESTÃO 4
Existem outras razões trigonométricas que são idênticas?
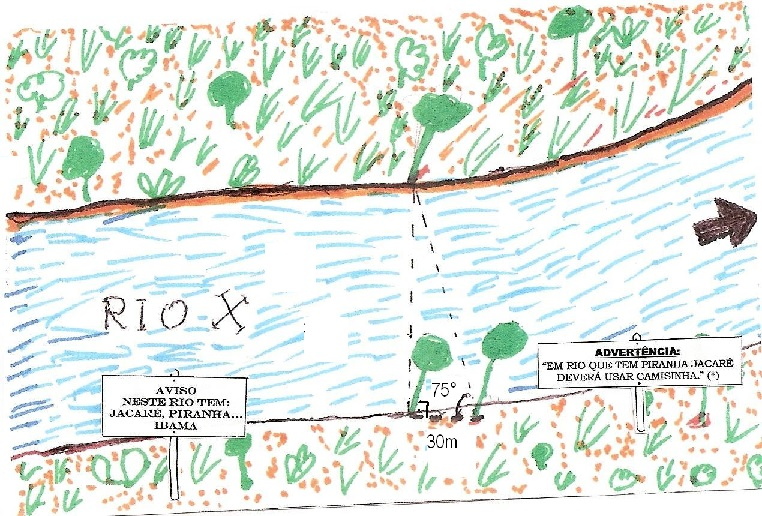
QUESTÃO 5
O usando que foi visto nesta apresentação determinar a largura, aproximada, do Rio X, do esboço anterior:
RESUMO:
Apresentam-se algumas chaves ou macetes, as chaves, numa perspectiva otimista, são indicativos de: abertura, liberdade, novos rumos, alternativas inovadoras, como elemento facilitador para resolver as atividades que envolvem relações (razões)trigonométricas no triângulo retângulo:
CHAVE 1
Se a relação envolve catetos: Cateto oposto sobre cateto adjacente usa-se: tangenteou cateto adjacente sobre cateto oposto emprega-se:cotangente.
CHAVE 2
Se a relação envolve hipotenusa: Cateto oposto ao ângulo usa-se:seno ou cateto adjacente ao ângulo usa-se cosseno.
CHAVE 3
Se a incógnita (variável, valor procurado) da razão trigonométrica é o antecedente (numerador, está em cima) multiplica-se o denominador (consequente, está em baixo) pelo valor trigonométrico do ângulo.
CHAVE 4
Se a incógnita da razão trigonométrica é o consequente (denominador, está em abaixo) divide-se o antecedente (numerador, está em cima) pelo valor trigonométrico do ângulo.
ATIVIDADE DESAFIADORA:
Completar a Tabela trigonométrica empregando os recursos da Planilha e os critérios já executados:
CULMINÂNCIA:
Semelhança em geometria euclidiana mantem uma conexão intrínseca com razões e proposições em álgebra e vice-versa.