1.05 Exploratory Challenge Day 2
The incenter of a triangle is the center of a triangle's "incircle" (the circle that fits perfectly inside triangle, just touching all sides) It is where the "angle bisectors" (lines that split each corner's angle in half) meet.
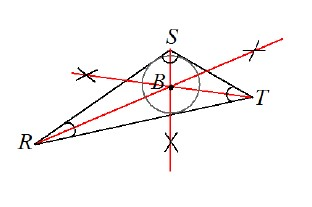
Draw a triangle of your own below and construct the incenter.
The circumcenter of a triangle is the center of a triangle's circumcircle. It is where the "perpendicular bisectors" (lines that are at right angles to the midpoint of each side) meet.
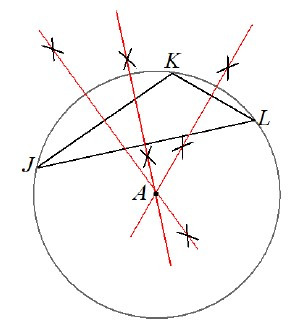
Draw a triangle of your own below and construct the circumcenter.
What have you learned in the task above to find the center of a circle if the center is not shown?