Vectores ortogonales
Introduccion.
Supongamos que tenemos dos vectores A y B, si ambos están separados por un ángulo θ, podemos determinar el valor de éste último mediante la fórmula:
=&space;\frac{\mathbf{A}&space;\cdot&space;\mathbf{B}}{\left&space;|&space;\textbf{A}&space;\right&space;|\left&space;|&space;\textbf{B}&space;\right&space;|})
Si los vectores son perpendiculares entre sí, es decir, θ = π/2, entonces:
=&space;\frac{\mathbf{A}&space;\cdot&space;\mathbf{B}}{\left&space;|&space;\textbf{A}&space;\right&space;|\left&space;|&space;\textbf{B}&space;\right&space;|}&space;=&space;0)
De aquí que:
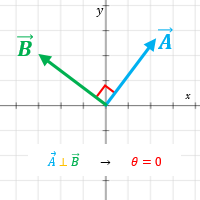
En consecuencia dos vectores son perpendiculares u ortogonales si forman un ángulo recto (θ = π/2) y por ende, su producto escalar es cero.
Definiciòn.
Cuando dos vectores A = (Ax, Ay, Az) y B = (Bx, By, Bz) son perpendiculares entre sí, es decir, forman un ángulo recto (θ = π/2), se dice que son vectores ortogonales. Esta situación se denota como A ⊥ B. Dos vectores serán ortogonales cuando su producto escalar (también llamado producto punto y producto interno) es cero:
A ⊥ B → A · B = AxBx + AyBy + AzBz
O
A ⊥ B → θ = π/2 → A ∙ B = |A| |B| cosθ = 0
Ya que cos (π/2) = 0.
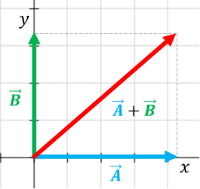
Cuando dos vectores de A y B son ortogonales, forman un triángulo rectángulo, cuya hipotenusa es igual a la suma de los vectores.
Ejercicios Resueltos.
- Determinar si los vectores A = (1, 2) y B = (-2, 1) son ortogonales.