Función Inyectiva
1.7 Función inyectiva
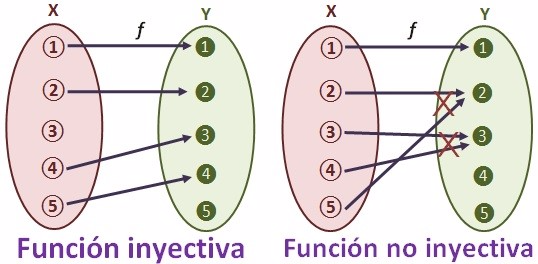
La función f es inyectiva si cada elemento del conjunto final Y tiene como máximo un elemento del conjunto inicial X al que le corresponde. Es decir, no pueden haber más de un valor de X que tenga la misma imagen y.
Supuesto de aplicación
Algunos ejemplos de la vida cotidiana son:
- Cuando conectas en una amplificador los cables, no todos los orificios van a quedar
- Cuando se asignan identificadores de usuarios, a cada usuario le corresponde un único
¿Qué podemos ver en el applet?
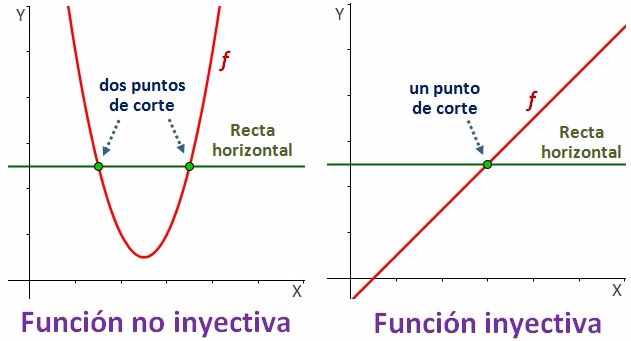
La prueba de la recta horizontal se realiza para comprobar si una función es o no inyectiva. Consiste en dibujar una recta horizontal paralela al eje de abscisas y ver en cuántos puntos corta dicha recta a la gráfica.
Si encontramos alguna recta horizontal que corta a la gráfica en dos o más puntos, la
función no es inyectiva.
En cambio, si todas las rectas horizontales cortan en un máximo de un punto, la función
es inyectiva.
En el applet podemos ver que la pelota está tocando las dos manos del jugador por lo que tiene dos puntos de corte y esto hace que sea una función no inyectiva.
¿Cómo funciona el applet?
Teniendo en cuenta que la trayectoria de la pelota es la función, con el deslizador se podrá jugar con
ella y observar si es o no una función inyectiva