Teorema de Pitágoras
Breve biografía
James Abram Garfield (1831-1881) fue el vigésimo presidente de los Estados Unidos. Fue elegido presidente en marzo de 1881, pero en septiembre del mismo año falleció a causa de las heridas provocadas por unos disparos que había recibido un par de meses antes.
Antes, en 1876, descubrió esta demostración del teorema de Pitágoras que fue publicada en el 'New England Journal of Education'.
CONSTRUCCIÓN DE GARFIELD
Garfield giró +90º un triángulorectángulo en el sentido de las agujas del reloj y de centro el vértice de
ángulo menor, como indicamos a continuación:
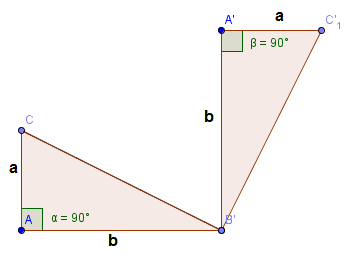
A este triángulo fruto del giro del original le aplicó una traslación de vector la hipotenusa del primer triángulo, de esta forma:
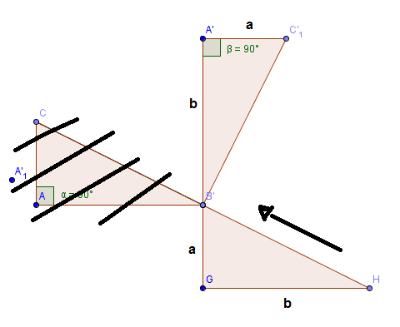
Uniendo los dos vértices obtuvo un trapecio rectángulo como el del siguiente dibujo:
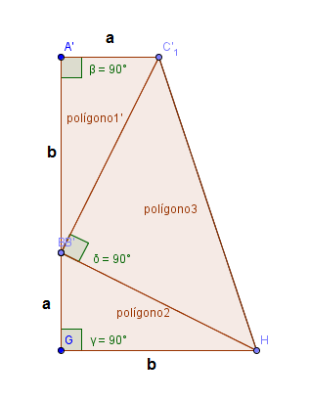
Garfield calculó, primeramente, el áreadel trapecio resultante mediante la conocida fórmula del área del
trapecio
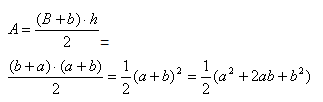
Después, Garfield calculó el área de cada uno de los 3 triángulos que componen el trapecio de la figura, mediante la conocida fórmula del área de un triángulo
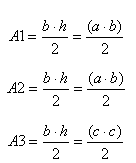
Siendo “c” la hipotenusa de cada uno delos 2 triángulos rectángulos que forman el trapecio. Posteriormente, sumó las 3 áreas con la intención de obtener el área total del trapecio, que está compuesto por los 3 triángulos, así:
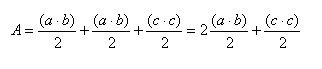
Aclaración: el 2/2 se va y nos queda
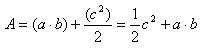
Para terminar, si igualamos el área del trapecio obtenida mediante su fórmula correspondiente, y ésta última obtenida mediante la suma de las áreas de los 3 triángulos que componen el trapecio, obtenemos lo siguiente:
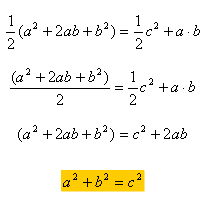
Y se obtiene la expresión del Teorema de Pitágoras; El cuadrado de la hipotenusa (c) es igual a la suma del cuadrado de los catetos (a y b)