Numeri naturali (ℕ) e interi relativi (ℤ)
- Tramite il punto unità (ossia il numero 1) e l'addizione si definiscono 2:=1+1, 3:=2+1,... e così via, permettendo di ottenere l'insieme N dei numeri naturali: N := {0,1,2,3,...}; mediante l'opposizione si ottiene l'insieme dei numeri interi relativi: Z := {0,1,-1,2,-2,3,-3,...}
- moltiplicazione a coefficienti interi :
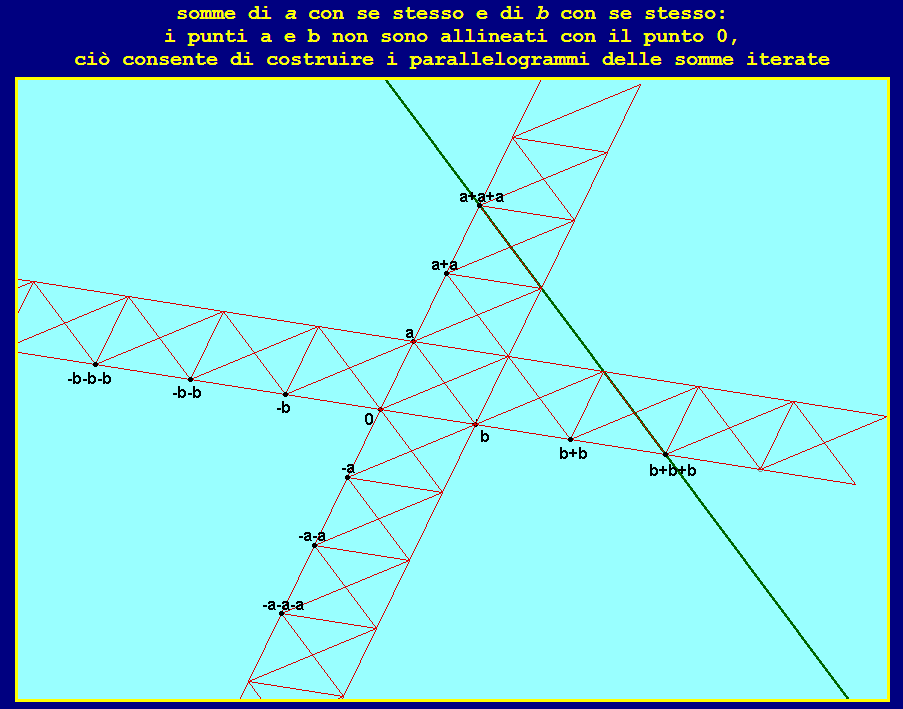
come da 1 si ottengono i numeri interi, partendo da un punto z si
possono produrre i punti z+z, z+z+z, ecc... e i loro opposti; ciò
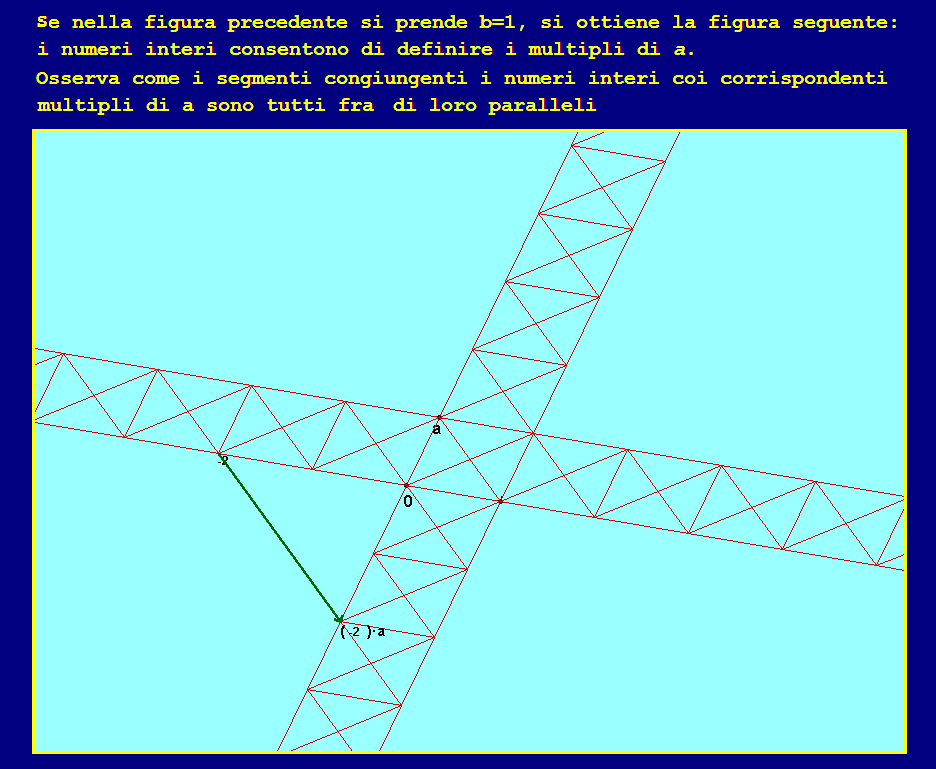
conduce a definire un'operazione, detta moltiplicazione a coefficienti interi: 1z:=z, 2z:=z+z, 3z:=2z+z, ecc..., (-1)z:=-z, (-2)z:=-2z, (-3)z:=-3z, ecc..., completandone la costruzione con la definizione 0z := 0
- le proprietà di base della moltiplicazione a coefficienti interi, dimostrabili a partire
dalla definizione di tale tipo di moltiplicazione e dai quattro assiomi additivi enunciati
precedentemente, e dalle quali possono essere dedotte altre proprietà
(teoremi), sono:
- neutralità dell'uno: 1 z = z
- associativa: m ( n z ) = ( m n ) z
- distributiva a sinistra: n ( z + w ) = n z + n w
- distributiva a destra: ( m + n ) z = m z + n z .