Dürer 2
Op de vorige bladzijde tekent Dürer wel een correcte ellips door een cirkelboog uit te rekken.
Alleen, hij weet niet dat het een ellips is.
Dat een verlengde halve cirkel een ellips is, wordt pas in 1640 ontdekt door Paul Guldin (1577-1643), een Zwitserse jezuïet, wiskundige en astronoom die ook contacten had met Johannes Kepler.
constructie
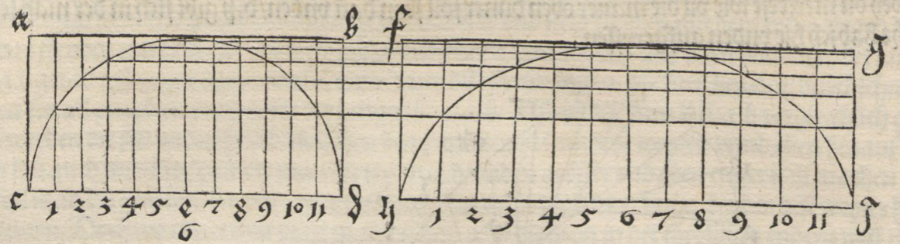
- Teken binnen een rechthoek ABCD een halve cirkel.
- Teken in de rechthoek verticale lijnen en verdeel de recthoek in twaalf gelijke verticale stroken.
- Teken naast de rechthoek ABCD een tweede rechthoek EFGH, breder dan de eerste en verdeel ook deze rechthoek in twaalf gelijke verticale stroken.
- Bepaal de snijpunten van de cirkel met de verticalen en teken horizontale lijnen door deze snijpunten.
- Bepaal in de rechthoek EFGH de snijpunten van de horizontale en de verticale lijnen en verbind ze door een vloeiende kromme.