Copia de Secciones cónicas
Breve introducción histórica
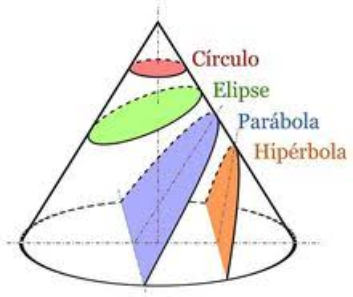
Eratóstenes atribuye a Menecmo, miembro de la escuela platónica (s. IV a.C.), el descubrimiento de las secciones cónicas. Este las introdujo utilizando tres tipos de conos según el ángulo en el vértice y cortando cada uno de ellos por un plano perpendicular a una generatriz: recto (parábola), agudo (elipse) y obtuso (hipérbola, conociéndose sólo una rama de la misma).
Apolonio de Perga (260 - 200 a.C.) publicó un tratado denominado Secciones cónicas en el que cambió el enfoque: obtuvo las secciones cónicas a partir de un mismo cono circular, de abertura arbitraria, por planos diversamente inclinados respecto al eje del cono. Según las distintas posiciones relativas del cono y el plano que lo corta aparecían distintos tipos de cónicas, siendo el primero que dio a las secciones cónicas los nombres de parábola, elipse e hipérbola, hasta entonces llamadas secciones recta, acutángula y obtusángula.
En la obra de Apolonio se encuentran todas las propiedades conocidas sobre diámetros, ejes, centro, asíntotas... Las 487 proposiciones en su tratado fueron demostradas a partir en el contexto del sistema axiomático de Euclides.
La potencia del tratamiento algebraico de la geometría, introducido por Descartes, llevó a John Wallis en De sectionibus conicis (1655) a deducir las ecuaciones de las cónicas traduciendo las condiciones geométricas de Apolonio a la forma algebraica. Definió las cónicas como las curvas correspondientes a ecuaciones de segundo grado en dos variables, y probó que ésas eran efectivamente las secciones cónicas usuales de la geometría. Su estudio popularizó su tratamiento como curvas en el plano en vez de como secciones de un cono.