Rectas y puntos notables en los triángulos

En esta actividad aprenderemos que son las rectas notables y los puntos que estas forman cuando se interseca, asi como ejercicios relacionados.
Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo.
Además, dos lados contiguos forman uno de los ángulos interiores del triángulo que, como su propio nombre indica, tiene tres. Y, como es bien sabido, la suma de éstos es 180º.
Mediatrices y circuncentro
Las mediatrices de un triángulo son las mediatrices de sus lados, es decir, las rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos.
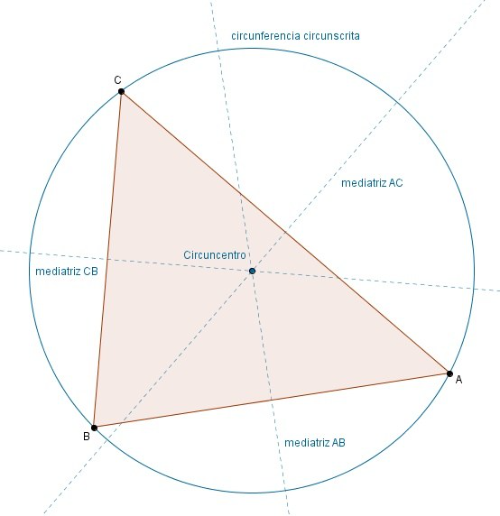
La mediatriz de un segmento cualquiera es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de los puntos extremos de dicho segmento. En el caso del lado de un triángulo es, por tanto, el lugar geométrico de los puntos que equidistan de los vértices de dicho lado.
Las tres mediatrices del triángulo (hay una por cada lado) se cortan en un punto que está, por tanto, a la misma distancia de los tres vértices del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que pase por los tres vértices. A esa circunferencia se la denomina circunferencia circunscrita, y al centro de la misma en el que se cortan las tres mediatrices circuncentro.
Propiedad:
"Los puntos de la mediatriz de un lado de un triángulo equidistan de los vértices
que definen dicho lado"
Ejercicios con mediatriz
Bisectrices e incentro
Las bisectrices de un triángulo son las bisectrices de sus ángulos. Existen bisectrices internas (las usuales) y externas a estos ángulos, y son perpendiculares entre sí.
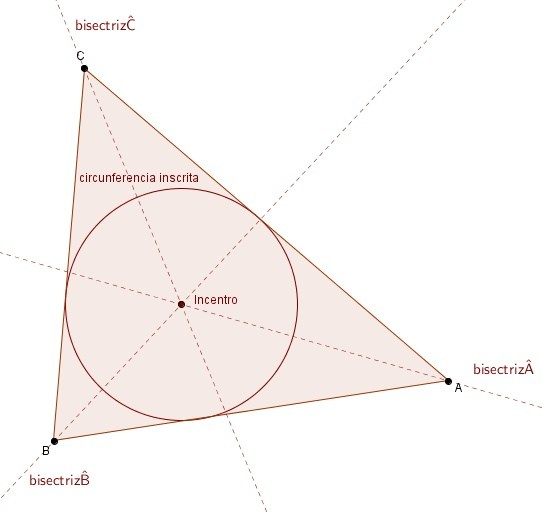
La bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.
Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.
Propiedad:
"Los puntos de la bisectriz equidistan de los lados del ángulo"
Es decir: si trazamos perpendiculares desde un punto a los dos lados, los segmentos que se
forman son de la misma longitud.
Ejercicios con bisectriz
Medianas y baricentro
Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.
Las tres medianas de un triángulo se cortan en un punto llamado baricentro.
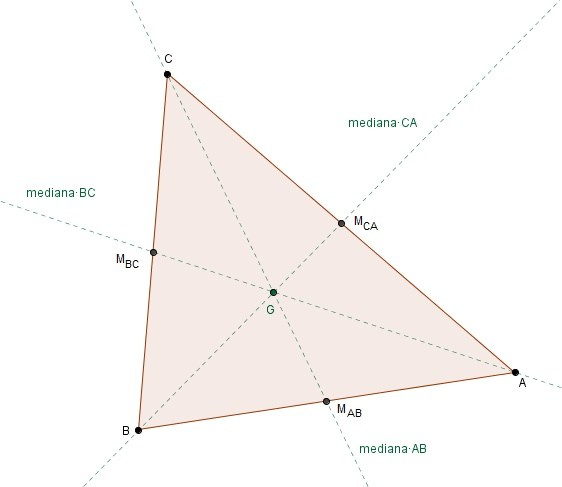
Cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.
Propiedades:
"Las tres medianas de un triángulo son interiores al mismo, independientemente
del tipo de triángulo que sea"
"Cada mediana de un triángulo divide a éste en dos triángulos de igual área"
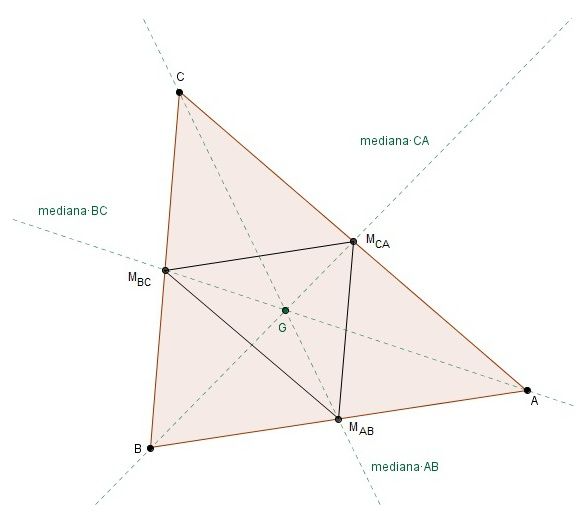
También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.
Ejercicios con mediana
Alturas y ortocentro
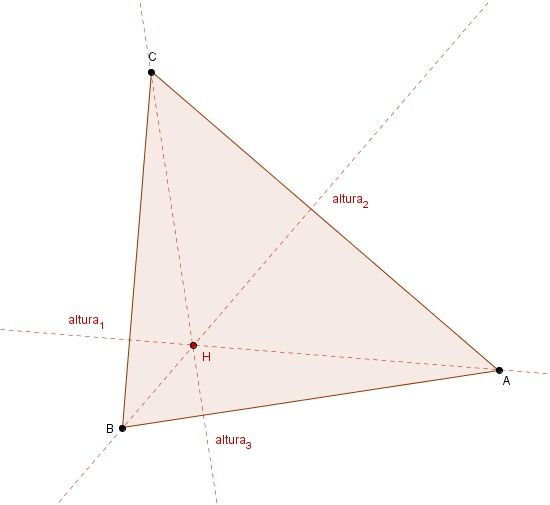
Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.
Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.
Propiedades:
Una altura puede ser interior al triángulo, exterior al mismo, o incluso, coincidir con
alguno de sus lados (según el tipo de triángulo):
Si el triángulo es RECTÁNGULO:
"La altura respecto a la hipotenusa es interior, y las otras dos alturas coinciden
con los catetos del triángulo"
Si el triángulo es ACUTÁNGULO:
"Las tres alturas son interiores al triángulo"
Si el triángulo es OBTUSÁNGULO:
"La altura respecto al mayor de sus lados es interior, siendo las otras dos alturas
exteriores al triángulo"
"En un triángulo isósceles, la altura correspondiente al lado desigual divide el
triángulo en dos triángulos iguales"
Ejercicios con la altura de un triángulo
Recta de Euler
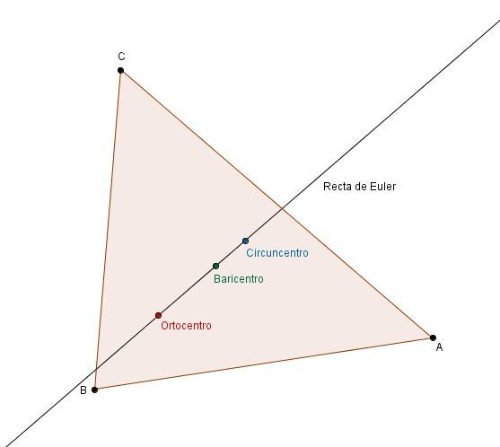
La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo.
Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.
FELICIDADES!!!!!!! has llegado hasta aquí; pero si aun no has comprendido bien aquí un vídeo para que refuerces tus conocimientos:
Buen trabajo has aprendido todo el material de la lección; ahora vamos a interactuar con las rectas y puntos notables de un triangulo en el plano:
¿Como interactuar con la hoja dinámica? Selecciona la recta o punto notable que quieras observar así como las relaciones entre estos que quieras. Sencillo!!!!
Vamos a resolver!
Calcular la altura, que divide al triángulo equilátero en dos triángulos rectángulos cuya base es la mitad que la base del triángulo original:

En un triángulo A, B, C, el segmento AC, mide 8cm y la mediatriz de AC, interseca a AB en M y a CA, en D. Además, la medida del segmento MD, D es 3cm. ¿Cuál es la longitud del segmento AM?
¿Que recta notable pertenece a la imagen?
¿Que recta notable pertenece a la imagen?