enkele extra's
Over de praktijk van luisteren, uitvoeren en stemmen valt nog heel wat meer te zeggen en te onderzoeken.
Op deze pagina lees je iets meer over volgende onderwerpen:
- het melodisch denken en psychologie van uitvoerder en luisteraar
- waargenomen boventonen verschillen van theoretisch model
- psychoakoestiek
- kwinten in hoogste octaven
- een pianostemmer moet oren hebben
het melodisch denken en de psychologie van uitvoerder en luisteraar
Een mens denkt niet gelijkzwevend. Een pianist is gebonden aan de stemming van zijn piano, maar zangers
en violisten niet. Nauwkeurige metingen van opnames van beroemde uitvoerders tonen aan dat ze in bepaalde intervallen duidelijk afwijken van de theoretische toon binnen een gelijkzwevende stemming, zonder dat de toehoorder een 'valse' toon waarneemt. Strijkkwartetten, blokfluit- en gambaconsorts zoeken reine verhoudingen op.
Reeds in zijn boek 'Harmonics or the Philosophy of musical Sounds' uit 1749 schrijft de Engelse wiskundige en astronoom Robert Smith na heel wat berekeningen en uitweidingen over stemmingen en toonaarden doodleuk:
"The several parts of a concert wel performed upon perfect instruments do not move exactly by the given intervals of any system whatever, but only pretty nearly, and so as to make perfect harmony as near as possible... Now the reason why the best performers acquire a habbit of making perfect harmony as near as possible is plainly this. When the harmony is made perfectly they are pleased and satisfied."
Je vindt het hele boek in facsimile online op Harmonics - Robert Smith
Bovenstaand fragment en verdere uitwijdingen over de muziekpraktijk vind je pag. 225 e.v.
M.a.w. een goede muzikant speelt met zijn oren en niet volgens ingewikkelde temperingen en formules.
Voilà, van relativeringsvermogen gesproken...
Smith doet er zelfs nog een schepje bovenop met de raad "nooit gezongen partijen mee te spelen met het orgel, tenzij om een 'imperfecte' zanger te begeleiden en hem zo er van te behoeden om nog slechtere samenklanken te zingen dan het orgel zelf speelt."
Er is in de muziekpraktijk geen onomstotelijk vastliggende dogma voor een juiste intonatie en het menselijk oor vraagt het niet. Tot er moet samengespeeld worden met een piano natuurlijk...
Geen wonder dat Beethoven de gelijkzwevende stemming helemaal niet zag zitten en Maurice Ravel ronduit zei dat een viool en een piano niet konden samenspelen.
waargenomen boventonen verschillen van theoretisch model
Een theoretisch wiskundig model is een, in de praktijk duiken voortdurend randvoorwaarden op.
Geef een speelgoedautootje een zetje, zodat het begint te rollen.
De theorie zegt dat, wanneer er geen kracht wordt op uitgeoefend, het zal blijven voortrollen aan dezelfde snelheid.
Maar door de wrijving van de wieltjes en de rolweerstand met vloer of tafel, zal het niet ver bollen.
En begin die weerstanden maar eens te berekenen...
Zo is het ook met snaren. Een snaar heeft materie. Bij het strijken of plukken van een snaar wordt ze uitgerekt.
De vervorming roept een weerstand op in het materiaal en die stijfheid van een snaar heeft als gevolg dat de waargenomen
boventonen hoger klinken dan de berekende tonen in het theoretisch harmonisch model.
De afwijkingen nemen bovendien toe naarmate je verder gaat in de rij van harmonische tonen. M.a.w. hoe hoger de boventoon
hoe groter de afwijking. Deze boventonen veroorzaken een conflict met de tonen in de verst van het midden verwijderde octaven
van een piano.
psychoakoestiek
De psychoakoestiek onderzoekt hoe tonen worden waargenomen.
Het blijkt duidelijk dat hogere tonen als lager worden waargenomen dan hun reële toonhoogte.
De toonhoogte van een (zuivere) toon kan ook geschat worden.
De resulterende toonhoogteschaal heet de mel-schaal.
Het verband tussen toonhoogte (mel) en frequentie (Hz) dat men zo krijgt is afgebeeld in onderstaande figuur.
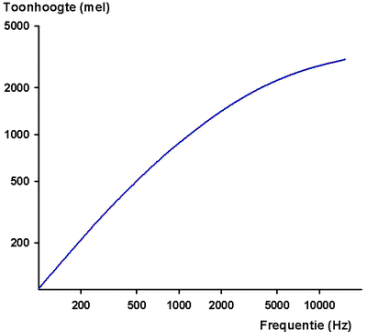Voor frequenties onder de 1000 Hz lopen toonhoogte (in mels) en frequentie (in Hz) gelijk.
Rond de 1000 Hz treedt een overgang op naar een logaritmisch verband. Dit betekent dat de toonhoogte, uitgedrukt in mels, steeds minder gaat toenemen wanneer de frequentie toeneemt. Het verschijnsel is hoorbaar bij de hoogste octaven van een piano.
Het plaatje is eigenlijk nog ingewikkelder, omdat de subjectieve toonhoogte ook afhangt van de luidheid van de toon. Een toon van 1000 Hz behoudt zijn subjectieve hoogte, onafhankelijk van de luidheid.
Voor lage tonen geldt: hoe luider hoe lager, voor hoge tonen hoe luider hoe hoger de subjectieve toonhoogte. Bovendien is de relatie tussen luidheid en toonhoogte anders voor sinustonen dan voor complexere (harmonische) tonen...
Een bijkomend psychoakoestisch verschijnsel dat we kwijtraakten met de gelijkzwevende stemming zijn de verschiltonen, waarbij we bij harmonisch samenklinkende tonen een derde toon lijken te horen, met als frequentie het verschil van de frequenties. Voorbeeld: een la (440 Hz) en een mi (660 Hz) brengen een verschiltoon voort van 220 Hz. Dit toon wordt niet gespeeld, het zijn onze hersenen die deze bijkomende toon produceren. Maar wanneer je harmonische tonen opgeeft om het toonsysteem eenvoudiger te maken, verlies je dit fenomeen.
Luister maar eens naar een gamba consort dat in reine stemming renaissance muziek speelt...
M.a.w. Geluidswaarneming wordt niet alleen bepaald door wat muzikanten echt spelen.
Ook onze oren en onze hersenen spelen een belangrijke rol.
Voor frequenties onder de 1000 Hz lopen toonhoogte (in mels) en frequentie (in Hz) gelijk.
Rond de 1000 Hz treedt een overgang op naar een logaritmisch verband. Dit betekent dat de toonhoogte, uitgedrukt in mels, steeds minder gaat toenemen wanneer de frequentie toeneemt. Het verschijnsel is hoorbaar bij de hoogste octaven van een piano.
Het plaatje is eigenlijk nog ingewikkelder, omdat de subjectieve toonhoogte ook afhangt van de luidheid van de toon. Een toon van 1000 Hz behoudt zijn subjectieve hoogte, onafhankelijk van de luidheid.
Voor lage tonen geldt: hoe luider hoe lager, voor hoge tonen hoe luider hoe hoger de subjectieve toonhoogte. Bovendien is de relatie tussen luidheid en toonhoogte anders voor sinustonen dan voor complexere (harmonische) tonen...
Een bijkomend psychoakoestisch verschijnsel dat we kwijtraakten met de gelijkzwevende stemming zijn de verschiltonen, waarbij we bij harmonisch samenklinkende tonen een derde toon lijken te horen, met als frequentie het verschil van de frequenties. Voorbeeld: een la (440 Hz) en een mi (660 Hz) brengen een verschiltoon voort van 220 Hz. Dit toon wordt niet gespeeld, het zijn onze hersenen die deze bijkomende toon produceren. Maar wanneer je harmonische tonen opgeeft om het toonsysteem eenvoudiger te maken, verlies je dit fenomeen.
Luister maar eens naar een gamba consort dat in reine stemming renaissance muziek speelt...
M.a.w. Geluidswaarneming wordt niet alleen bepaald door wat muzikanten echt spelen.
Ook onze oren en onze hersenen spelen een belangrijke rol.kwinten in de hoogste octaven
Dat reine kwinten en reine octaven niet samen gaan, dat wist je al.
Voor een la met een frequentie van 440 Hz is de gelijkzwevende stemming geen probleem.
Een reine kwint van deze toon heeft een frequentie van 440 . 3/2 = 660 Hz.
Een gelijkzwevende kwint van deze toon heeft een frequentie van 440 . 2(7/12) = 659.3 Hz.
Dit verschil van 0.7 Hz is niet waarneembaar door het menselijk oor.
Het waarneembare verschil tussen toonhoogten (= de frequentieresolutie) bedraagt ongeveer 2 Hz.
Maar elk octaaf hoger zal dit verschil verdubbelen.
Je merkt dat het verschil tussen de reine en de gelijkzwevende kwint al snel merkbaar wordt.
| la | . 3/2 | . 2(7/12) | verschil |
| 440 Hz 880 Hz 1760 Hz 3520 Hz | 660 Hz 1320 Hz 2640 Hz 5280 Hz | 659.3 Hz 1318.5 Hz 2637 Hz 5274 Hz | 0.7 Hz 1.5 Hz 3 Hz 6 Hz |
een pianostemmer moet oren hebben
Heb je geen ervaring in het stemmen van een piano probeer je het zelf een eenvoudig stemapparaatje, dan zal het resultaat pover zijn, ook al is er niets mis met het apparaatje.
Het probleem is het verschil tussen het theoretisch model van de gelijkzwevende stemming zelf en de praktijk. Hogere tonen klinken te laag, boventonen klinken te hoog en gelijkzwevende kwinten komen te laag uit...
Een pianostemmer gaat daarom de uiterste octaven van het pianoklavier lichtjes uitrekken.
De hoogste tonen wordt hoger gestemd dan in het theoretische model, de laagste lager.
De stijfheid van snaren is materiaaleigen. Ze is ook belangrijker in kortere piano's dan in langere.
En ook de psychoakoestiek laat zich niet zomaar vertalen in vaststaande formules.
We kunnen wel berekenen hoeveel groter je een octaaf moet maken om een kwint rein te maken.
De vergelijking wordt: x7/12 = 1.5
De oplossing is x = 1.512/7 = 2.0039
Pas je dit bv. toe op een la van 1760 Hz, dan wordt het octaaf 1760 . 2.0039 = 3526.8 Hz i.p.v. 3520 Hz.
De kwint van een la 1760 Hz wordt nu wel perfect rein.
De net iets hoger gestemde tonen klinken ook aangenamer en briljanter.
Een pianostemmer moet niet alleen een pianosleutel hebben en een stemapparaat, maar vooral oren.
Niet alleen Pythagoras stuitte op de grenzen van een mooi theoretisch model...
Ook het wiskundig model van de gelijkzwevende stemming heeft zijn grenzen.
Pianofabricant Steinway heeft zijn topstemmers, concerthuizen laten niet de eerste de beste stemmer komen. Sommige concertpianisten zweren bij een vaste stemmer, terwijl de Franse toppianist Alexandre Tharaud zelfs geen piano heeft staan. Hij oefent bij vrienden om zich niet te fixeren op het geluid van één piano op één plaats.