Quadratic Approximation in Single Variable Case
At a stable point, the first-order derivative tells us nothing interesting. What about the second? The second-order derivative is the derivative of the derivative. In the single variable case, it gives the changing rate of the tangent line's slope at a point. If the slope increases as increases, it means that this stable point is a local minimum; if the slope decreases, it means that this stable point is a local maximum. We can only identify local minima or maxima, not the global ones because the second-order derivative gives us only the information of the function in a very small range near the analyzed point.
A quadratic approximation of a function at some point satisfies the following properties:
1. is a quadratic function;
2. goes through this point;
3. its first-order derivative at this point is equal to the function's first-order derivative at this point;
4. its second-order derivative at this point is equal to the function's second-order derivative at this point.
So the quadratic approximation of at is:
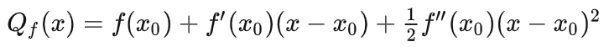
You can verify that this function satisfies all the properties above. In fact, this is called the second-degree Tayler polynomial. Here is a brief introduction to the Tayler polynomials. The th Tayler polynomial has terms and is of degree . Its th-order derivative is equal to the function's th-order derivative for every positive integer . Also, as increases, the Taylor polynomial approximates the original function better and better.
Getting back to our problem, the quadratic approximation is pretty close to the function at the analyzed point, as shown in the graph. At most times, the quadratic approximation would give us enough information to decide whether the given stable point is a local maximum or local minimum. To make things easier, the first-order derivative of the function at a stable point is 0, so our quadratic approximation reduces to:
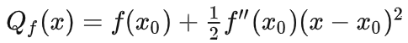
Therefore is also a stable point for the quadratic approximation. If our is a maximum on the quadratic approximation, then it's a local maximum on the original function. The same is as with a minimum.