Aufstellen von Polynomfunktionen
Der Graph einer Polynomfunktion vom Grad 3 hat einen Tiefpunkt bei und einen Wendepunkt bei . Ermittle eine Termdarstellung dieses Polynoms.
Musterlösung:
1) Allgemeine Termdarstellung inkl. 2 Ableitungen (bis f'' wegen Wendepunkt):
2) Bedingungen verwerten (es werden 4 Koeffizienten (a, b, c, d) gesucht, also werden auch 4 Bedingungen benötigt):
3) Gleichungssystem Lösen:
4) Koeffizienten einsetzen:
______________________________________________________________________________________
Lösung mit Geogebra:
- CAS-Ansicht öffnen
- Allgemeinen Funktionsterm definieren (beachte ":=", sowie die Verwendung eines Malpunktes "*" ): f(x):=a*x^3+b*x^2+c*x+d
- Verwende Befehl Löse( ): "Löse[{f(0)=2, f'(0)=0, f(-1)=12, f''(-1)=0}, {a, b, c, d}]"
- Verwende Befehl (beachte die Verwendung #2 um die Ausgabe von Zeile 2 zu kopieren) Ersetze( ): "Ersetze[f , #2 ]"
______________________________________________________________________________________
Aufgabe:
Gegeben ist der Graph einer Polynomfunktion. Ermittle den Grad sowie Funktionsterm der Funktion.
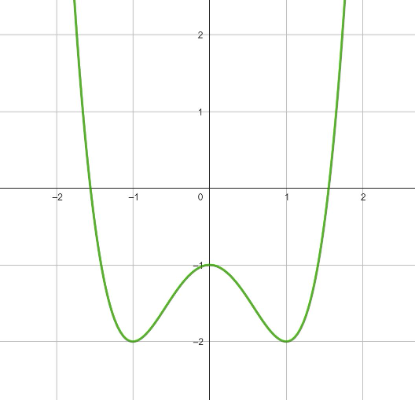
kleinstmöglicher Grad der Polynomfunktion:
Aufstellen des Funktionsterms mit Geogebra: