Ecuación de la recta

Szerző:Fernanda

DEFINICIÓN DE RECTA

Definimos a una recta

como el conjunto de los puntos del plano, alineados con un punto

y con una dirección dada

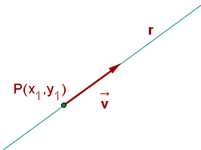
ECUACIÓN DE LA RECTA QUE PASA POR UN PUNTO

Para determinar la expresión algebraica de la recta que pasa por un punto es necesario conocer la tanto la pendiente (m) como las coordenadas del punto (x,y).

Recordamos la ubicación del punto dentro del plano cartesiano se hace mediante el uso de coordenadas.

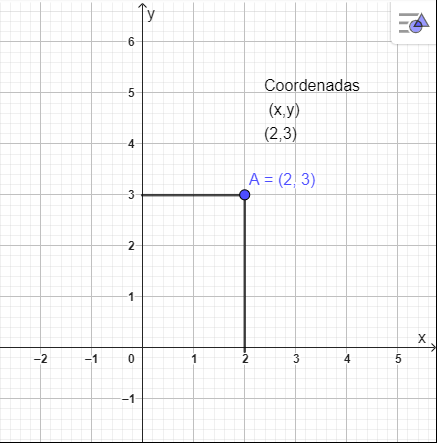
(x,y) es la manera en la que se debe escribir la ubicación del punto, por ejemplo el siguiente punto se encuentra ubicado en la coordenada (2,3) La ecuación de la recta que pasa por un punto es la manera más sencilla de todos los casos de las expresiones algebraicas relacionadas con la recta. La ecuación se escribe de la siguiente manera:

EJEMPLO Para determinar la ecuación de la recta que pasa por el punto (1,5) y tiene una pendiente igual a 3 ¿como determino la ecuación de la recta? Se aplica la ecuación general para las ecuaciones de la recta que pasan por un punto:

Conociendo la ecuación de la recta se reemplazan valores. x=1 ; y=5 ; pendiente (m)=3 5= 3.(1)+b 5-3=b 2=b En conclusión la ecuación de la recta que pasa por el punto (1,5) y tiene una pendiente igual a 3 es:

ECUACION DE LA RECTA QUE PASA POR DOS PUNTOS

Para determinar la ecuación de la recta que pasa por dos puntos es necesario conocer las coordenadas.

La ecuación de la recta será:

La fórmula para hallar la ecuación de la recta a partir de dos puntos cualesquiera P(x₁,y₁) y Q(x₂,y₂) es:

La fórmula de esta ecuación se deduce de la ecuación punto-pendiente de la recta:

Como la pendiente de una recta se puede calcular mediante la siguiente expresión

De esta manera, llegamos a la formula de la ecuación de una recta dadas las coordenadas de dos puntos pertenecientes a la recta.

AHORA RESOLVEMOS EL SIGUIENTE EJERCICIO. HALLAR LA PENDIENTE DE UNA RECTA QUE PASA POR DOS PUNTOS

Encontrar la pendiente de la recta que pasa por los puntos P(2,1) Y Q(8,5) Solución:

por lo tanto

;

A continuación sustituimos cada variable por su valor:

expresada la ecuación en su forma general

expresada la ecuación en su forma explicita

AHORA MANOS A LA OBRA!

Ejercicio Nº1

EJERCICIO Nº2 Determinar la recta que pasa por un punto y tiene como pendiente 4

A=(3.4)
B(-3,7)
C(-1,2)

Hagamos un breve repaso

La ecuación

que hemos visto se denomina "ecuación de la recta en forma explícita" y nos permite hallar dicha ecuación cuando conocemos la pendiente y la ordenada al origen. y=mx+b ,

m=pendiente y= intersección del eje y Encontremos ahora la ecuación de una recta que pasa por un punto determinado y tiene pendiente m. Cuando sólo conocemos la pendiente m y las coordenadas de uno de los puntos de la recta

, su ecuación es:

Esta ecuación recibe el nombre de forma punto -pendiente de la ecuación de la recta. RESOLVEMOS EL SIGUIENTE EJERCICIO A MODO DE EJEMPLO Halla la ecuación de la recta que pasa por el punto P(7,2) y tiene pendiente m=4 solucion: Sabemos que P(7,2) y m=4 entonces

Ahora sustituimos cada variable por su valor:

aplicamos distributiva en el segundo miembro de la desigualdad

esta es la ecuación en su forma general si despejamos "y" tenemos:

Ecuación en forma explicita

EJERCICIO Nº3 Hallar la pendiente de la recta que pase por dos puntos determinados. 1. A(1,8) y B(0,2) 2. M(4,5) y N(-1,-3) Graficar la pendiente utilizando GeoGebra.

EJERCICIO Nº4 Encuentre la ecuación de la recta que satisfaga las condiciones dadas

Pasa por (2,3) y tiene pendiente 5
Pasa por (-2,4) y tiene pendiente -1
Pasa por (1,7) y (3,5)