Використання моделей для знаходження площі, обмеженої кривою, за допомогою інструменту «Інтеграл».
Задача на побудову 1. Побудувати модель для обчислення площі виділеної області за допомогою інтеграла.
Навчальне дослідження 1. Побудуйте моделі для графічного розв’язку нерівностей,
наведених на рис.1 (радіус кола змінюється за допомогою слайдера).
![[i]Рис. 1[/i]. Приклади нерівностей з колом.](https://www.geogebra.org/resource/fah9fcrh/sBgCK8Sn0PTZQjGn/material-fah9fcrh.png)
Навчальне дослідження 2. Побудуйте
модель графічного розв’язку нерівностей, наведеного на рис.2 за таких умов: прямі
перетинаються в початку координат; кут їх нахилу змінюється за допомогою
слайдера a1; протилежні кути
перетину прямих завжди мають бути рівні між собою; радіус кола змінюється за
допомогою слайдера r.
![[i]Рис 2.[/i] Графічний розв’язок нерівностей для навчального дослідження 2.](https://www.geogebra.org/resource/m5jefe9m/2xaUyddzBmnekAMU/material-m5jefe9m.png)
Запишіть нерівність, графічний розв’язок якої є інвертованою областю відносно області на
рис.2.
Навчальне дослідження 3. Побудуйте
модель графічного розв’язку нерівності,
наведеного на рис.3, за таких умов: динамічні графіки синусоїди і косинусоїди дозволяють
змінювати амплітуди кривих за допомогою слайдерів.
![[i]Рис 3.[/i] Графічний розв’язок для навчального дослідження 3.](https://www.geogebra.org/resource/vzbbehm6/Zx5wZzk6baasxkhf/material-vzbbehm6.png)
Відповіді:
Навчальне дослідження 1:
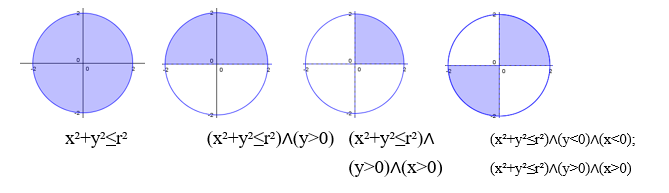
Навчальне дослідження 2:
(y ≤ a1 x) ∧ (x² + y² ≤ r²) ∧ (y ≥ -a1 x)
(y ≥ a1 x) ∧ (x² + y² ≤ r²) ∧ (y ≤ -a1 x)
(y ≤ a1 x) ∧ (x² + y² ≥ r²) ∧ (y ≤ -a1 x)
(y ≥ a1 x) ∧ (x² + y² ≥ r²) ∧ (y ≥ -a1 x)
Навчальне дослідження 3:
(y ≤ a cos(b x)) ∧ (y ≥ -a sin(b x))
(y ≥ a cos(b x)) ∧ (y ≤ -a sin(b x))