Discriminante de una ecuación cuadrática
Discriminante de una ecuación cuadrática o de segundo grado.
La forma general de una ecuación de segundo grado es
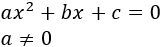Por comodidad, resolveremos la ecuación de tres formas distintas según los valores de los coeficientes b y c.
Se llama discriminante, Δ, a
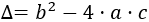El signo de Δ nos permite conocer el tipo de soluciones de la ecuación:
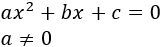Por comodidad, resolveremos la ecuación de tres formas distintas según los valores de los coeficientes b y c.
Se llama discriminante, Δ, a
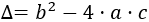El signo de Δ nos permite conocer el tipo de soluciones de la ecuación:
- Si Δ>0, hay dos soluciones reales distintas.
- Si Δ=0, hay dos soluciones reales iguales.
- Si Δ<0, no hay soluciones reales (hay dos soluciones complejas distintas).
Ejemplo 1
Determinar el tipo y número de soluciones de la ecuación
Solución
Calculamos el discriminante
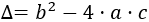Como los coeficientes son a=3, b=−5 y c=1, el discriminante es
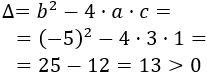El discriminante es positivo, así que la ecuación tiene dos soluciones reales distintas.
Solución
Calculamos el discriminante
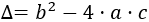Como los coeficientes son a=3, b=−5 y c=1, el discriminante es
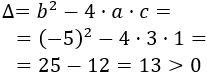El discriminante es positivo, así que la ecuación tiene dos soluciones reales distintas.Más información:
- Ecuaciones de segundo grado resueltas
- Ecuaciones bicuadradas resueltas
- Fracciones equivalentes y fracción irreductible
- Potencias (propiedades y ejercicios)
- Teorema de Pitágoras (con problemas resueltos)
- Ecuaciones de primer grado explicadas
- Problemas resueltos de ecuaciones
- Sistemas de ecuaciones (métodos)
- Problemas resueltos de sistemas de ecuaciones
- Problemas de progresiones o sucesiones
- Problemas resueltos de mcm y mcd
- Problemas resueltos de trigonometría (seno, coseno y tangente)
- Problemas de movimiento rectilíneo uniforme (MRU)
- Ecuaciones exponenciales resueltas
- Integrales resueltas (directas, por sustitución y por partes)
- Números complejos o imaginarios
- Problemas y Ecuaciones
- Logaritmos
- Teorema de Pitágoras online
- Calculadoras de porcentajes online