Schwerpunkt eines Dreiecks
Aufgabenstellung
Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der drei Seitenhalbierenden. Das ist der Punkt, an dem du ein Dreieck mit einem Finger von unten balancieren kannst, ohne dass es herunterfällt. Alternativ ist es auch der Punkt, an dem du das Dreieck aufhängen kannst, sodass es genau waagerecht (und damit parallel zum Boden) ausgerichtet ist.
Konstruiere mithilfe des GeoGebra-Applets (siehe unten) ein Dreieck mit den Eckpunkten
A(-5|-1), B(4|-2), C(2|3)
sowie den Schwerpunkt dieses Dreiecks. Die folgende Konstruktionsanleitung hilft dir dabei.
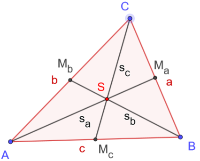
Konstruktionsanleitung
| 1 |  | Konstruiere das Dreieck ABC: Klicke auf das Werkzeug Vieleck und lege die Eckpunkte des Dreiecks in der Aufgabenstellung fest. |
| 2 |  | Zeige die Beschriftung der Punkte A,B,C und der Seiten a,b,c an: Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt um die Beschriftung anzeigen zu lassen. |
| 3 |  | Erzeuge die drei Mittelpunkte der Seiten des Dreiecks: Klicke auf das Werkzeug Mittelpunkt und anschließend auf zwei Punkte. |
| 4 |  | Zeichne die drei Seitenhalbierenden: Klicke auf das Werkzeug Strecke. Klicke auf einen soeben erzeugten Mittelpunkt und auf den der Seite gegenüberliegenden Eckpunkt des Dreiecks |
| 5 |  | Stelle die Seitenhalbierenden gestrichelt dar: Klicke auf das Werkzeug Bewege und anschließend mit links auf das entsprechende Objekt. Klicke auf die Gestaltungsleiste rechts oben und ändere die Darstellung des Objekts. |
| 6 |  | Beschrifte die Seitenhalbierenden mit sa, sb, sc: Klicke auf das Werkzeug Bewege und anschließend mit rechts auf das entsprechende Objekt um es umzubenennen. Um sa zu schreiben, stelle einen Unterstrich voran, etwa s_a. |
| 7 |  | Erzeuge den Schwerpunkt des Dreiecks: Klicke auf das Werkzeug Schnittpunkt und anschließend auf zwei der soeben konstruierten Seitenhalbierenden. |
Verständnisaufgaben bzw. -fragen
Bewege die Punkte A, B und C im GeoGebra-Applet um die folgenden Fragen zu beantworten.
Entscheide, ob die folgende Aussage wahr oder falsch ist: Jedes Dreieck besitzt genau einen Schwerpunkt.
Entscheide, ob die folgende Frage wahr oder falsch ist: Die drei Seitenhalbierenden des Dreiecks schneiden sich immer in genau einem Punkt.
Für welche Koordinaten der Punkte A, B und C liegt der Schwerpunkt genau im Koordinatenursprung ?
Entscheide, ob die folgende Frage wahr oder falsch ist: Der Schwerpunkt liegt immer innerhalb des Dreiecks
Welches Problem entsteht, wenn die Punkte A, B und C die Koordinaten ,und haben? Formuliere deine Beobachtung in einem Freitext.