6. La distancia de permutación dirigida
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
La distancia de permutación dirigida
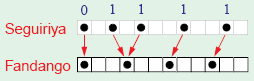
La distancia de permutación dirigida es una generalización de la distancia de permutación, pensada para tratar la comparación de patrones que no tienen el mismo número de acentos (unos). Por ejemplo, el fandango tiene cuatro acentos en lugar de cinco y, por tanto, esta generalización se hace necesaria. A continuación definimos formalmente esta distancia. Sean X e Y dos sucesiones binarias de longitud n que representan dos patrones. Se puede suponer, sin pérdida de generalidad, que X tiene más unos que Y . La distancia de permutación dirigida es el mínimo número de permutaciones necesarias para convertir X en Y bajo las siguientes condiciones:
- Cada “1” de X tiene que moverse a una posición “1” de Y.
- Todas las posiciones “1” de Y tienen que recibir al menos un “1” de X.
- Ningún “1” puede viajar a través de la frontera entre la posición cero y la n-ésima.
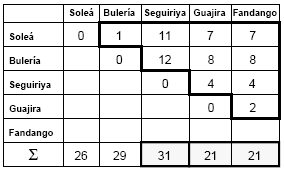
La búsqueda de algoritmos eficientes de computación para la distancia de permutación dirigida se encuentra actualmente bajo investigación. En el caso que nos ocupa, se pueden realizar los cálculos a mano obteniendo la siguiente matriz de distancias.