Ähnlichkeit und Strahlensätze (Dokumentation)
Einordnung in den Bildungsplan
Strahlensätze:
Die Strahlensätze werden laut Bildungsplan in der 7./8. Klasse behandelt. Dabei sollen Streckenlängen unter Nutzung der Strahlensätze bestimmt werden und die Nichtumkehrbarkeit des 2. Strahlensatzes mit Hilfe eines Gegenbeispiels begründet werden. Ersteres vermittelt nach Bildungsplan folgende Prozessbezogene Kompetenzen: Probleme lösen, Modellieren und Kommunizieren. Letzteres soll v.a. die Prozessbezogene Kompetenz Argumentieren und Beweisen schulen.
Für das Thema Strahlensätze sollten Schüler*innen folgende Vorkenntnisse haben:
- Lösen von Lineare Gleichungen durch Äquivalenzumformungen
- sicheres Nutzen von Maßstäben
- ein Verständnis von Streckenverhältnissen besitzen
- 2 gegebene Figuren mithilfe der jeweiligen Definition auf Ähnlichkeit zu untersuchen
- Dreiecke mithilfe ausgewählter Ähnlichkeitssätze (Übereinstimmung in den Längenverhältnissen aller Seiten, Übereinstimmung in 2 Winkelweiten) auf Ähnlichkeit zu überprüfen
- geometrische Zusammenhänge unter Verwendung bereits bekannter Sätze sowie mithilfe von Ähnlichkeitsbeziehungen zu erschließen, zu begründen und zu beweisen sowie Größen zu berechnen
Ähnlichkeit
Ähnlichkeit ist ein Begriff, den wir aus unserem Alltag kennen. Beispielsweise fällt uns auf, dass Gegenstände oder Personen ähnlich aussehen. Dabei kann es aber passieren, dass Person 1 zwei Menschen als ähnlich empfindet, währenddessen Person 2 dies nicht so sieht. D.h. Ähnlichkeit heißt für uns im Alltag in den wesentlichen Merkmalen übereinstimmend/ daran erinnernd. Es gibt also keine klaren Regeln an denen wir festhalten, ob etwas ähnlich oder nicht ähnlich ist.
In der Mathematik wollen wir aber klare Sätze, die uns ermöglichen eindeutig Ähnlichkeit zuweisen zu können. Daher ist es wichtig, Schüler*innen die Abgrenzung von Ähnlichkeit im Alltag und Ähnlichkeit in der Mathematik (entspricht dieselbe Form habend) zu verdeutlichen. So können Lehrkräfte falschen Vorstellungen zum Begriff vorbeugen. Dies kann schon durch ein kurzes Brainstorming zur Fragestellung "Was ist Ähnlichkeit im Alltag und was ist Ähnlichkeit in der Mathematik?" erreicht werden.
Konstruktion vor Instruktion
Da Schüler*innen schon intuitiv viel mit dem Begriff Ähnlichkeit anfangen können, ist es von Vorteil an dem aktuellen Wissenstand anzuknüpfen und neue Erkenntnisse anzuleiten.
Dafür eignet sich das Didaktische Prinzip Konstruktion vor Instruktion. Es besagt, dass Lernende erst selbstständig Inhalte erarbeiten bzw. entdecken sollen (Konstruktion), bevor der fertige aufbereitete Stoff vermittelt wird (Instruktion).
So haben Lernende die Möglichkeit, sich in der Konstruktionsphase aktiv mit dem Stoff zu beschäftigen und schon vorhandenes Wissen zu nutzen, um dieses dann auf neue Inhalte zu übertragen bzw. anzuwenden. In der Instruktionsphase werden dann die neu gewonnenen Erkenntnisse geordnet und sortiert, sodass für die Lernenden klar ist, was sie zu diesem Thema mitnehmen sollen.
Ähnlichkeit von Figuren
Im folgenden wird illustriert, wie eine Anwendung des Didaktischen Prinzips Konstruktion vor Instruktion an dem Thema Ähnlichkeit von Figuren aussehen kann.
Betrachten Sie den folgenden Ausschnitt aus dem Lehrbuch "Mathematikbuch 5" von Klett. Hier sind 14 A's in jeweils unterschiedlichster Form dargestellt. Die Aufgabe besteht darin, A's zu finden, die im geometrischen Sinne ähnlich sein könnten. (Zu diesem Zeitpunkt kennen die Schüler*innen den Satz für Ähnlichkeit von Figuren nicht.) Anschließend sollen die Schüler*innen beschreiben, worin sich die ähnlichen A's dennoch unterscheiden.
Nach Musterlösung sind folgende A's ähnlich zueinander: 2, 9, 12 und 5, 7, 14.
Durch die von der Aufgabenstellung angeleitete Diskussion in der Klasse wird deutlich, dass ein A gedreht, gespiegelt und/oder zentrisch gestreckt werden darf, damit es immer noch zum ursprünglichen A ähnlich ist.
Diese Erkenntnis ist sehr wertvoll, denn diese 3 Abbildungen sind schon fast alle Ähnlichkeitsabbildungen für Figuren.
Der Satz für Ähnlichkeit von Figuren lautet wie folgt:
Zwei Figuren sind ähnlich, wenn sie durch Drehung, Verschiebung, Spiegelung und Zentrischer Streckung aufeinander abgebildet werden können.
Somit haben sich die Schüler*innen nur anhand ihrer Intuition und ihrem Vorwissen den Satz für Ähnlichkeit von Figuren selbst hergeleitet (bis auf Verschiebung).
Nach dieser Konstruktionsphase ist es aber wichtig in die Instruktionsphase zu gehen, um jetzt den Satz für Ähnlichkeit von Figuren klar zu definieren. So stellt die Lehrkraft sicher, dass jedem der Satz klar ist und stellt aufbereiten Stoff zur Verfügung, mit dem jetzt weitergearbeitet werden kann (z.B. in Übungsphasen oder in der Vermittlung von darauf aufbauenden Inhalten).
Ähnlichkeit von n-Ecken
Der Satz für Ähnlichkeit von n-Ecken lautet wie folgt:
Zwei n-Ecke sind ähnlich zueinander, wenn ihre entsprechenden Winkel und ihre entsprechenden Seitenverhältnisse gleich groß sind.
Um diesen Satz nach dem Didaktischen Prinzip Konstruktion vor Instruktion zu vermitteln, kann folgende GeoGebra-Aktivität (Autor: bergerch, Florian Hansen) benutzt werden:
Zu dieser GeoGebra-Aktivität könnte ein Arbeitsauftrag für Schüler*innen wie folgt aussehen:
1) Im folgenden siehst du zwei ähnliche Dreiecke. Drehe, verforme, verschiebe und strecke zentrisch die Dreiecke. Was fällt dir auf? Finde Gemeinsamkeiten und Unterschiede bezüglich der 2 Dreiecke.
2) Stelle eine Vermutung auf, wann 2 beliebige Dreiecke ähnlich sind.
Nun werden Vor- und Nachteile genannt, wie gut sich diese Aktivität zur Vermittlung von Ähnlichkeit von n-Ecken eignet:
| Vorteile | Nachteile |
| - Prinzip Konstruktion vor Instruktion anwendbar - Drehung, Zentrische Streckung, Verschiebung (Abbildungen der Ähnlichkeitsabbildung) können auf Dreiecke angewendet werden | - Seitenverhältnisse nach Augenmaß abschätzen - selbstständiges Messen wird nicht geübt - werden nur Dreiecke veranschaulicht (andere n-Ecke werden nicht betrachtet) |
Ähnlichkeit von Dreiecken
Ein Dreieck ist zwar auch ein n-Eck, aber trotzdem geltem im Dreieck weitere Ähnlichkeitssätze:
![Quelle:[url=https://de.wikipedia.org/wiki/%C3%84hnlichkeitss%C3%A4tze][size=85][size=100] https://de.wikipedia.org/wiki/Ähnlichkeitssätze[/size][/size][/url]](https://www.geogebra.org/resource/gw4ymeyk/B9ulQ4VBriDKPhKc/material-gw4ymeyk.png)
In Schulbüchern werden meistens nur der WWW-Satz und der SSS-Satz vorgestellt.
Das Vorstellen aller Sätze bietet die Möglichkeit diese mit den Kongruenzsätzen (SSS, SWS, SSW, WSW) zu vergleichen und damit den Schüler*innen den Zusammenhang von Kongruenz und Ähnlichkeit zu verdeutlichen.
Dabei ist es wichtig klarzustellen, dass bei Kongruenzsätzen die Seitenlängen betrachtet werden, währenddessen bei den Ähnlichkeitssätzen nur die Seitenverhältnisse betrachtet werden. Das liegt daran, dass wir in der Kongruenz Identität wollen, währenddessen wir in der Ähnlichkeit zentrische Streckung zulassen. Außerdem ist eine wichtige Erkenntnis, dass 2 zueinander kongruente Dreiecke auch ähnlich zueinander sind.
Strahlensätze
Strahlensätze werden beispielsweise gebraucht um Höhen und Entfernungen zu bestimmen, wie folgendes Beispiel zeigt:
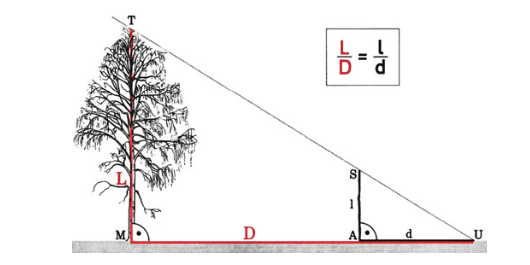
Hier soll die Baumhöhe bestimmt werden ohne die Höhe des Baumes tatsächlich zu messen. Da der Schattenwurf des Baumes bekannt ist, wird hier ein Stab so platziert, dass er zum einem parallel zum Baum ist und zum anderen der Schattenwurf des Stabes genau da endet, wo der Schattenwurf des Baumes aufhört. Somit ist D, d, l gegeben (siehe Bild) und die Höhe des Baumes kann mithilfe des 2. Strahlensatzes berechnet werden.
Die Strahlensätze lauten wie folgt:
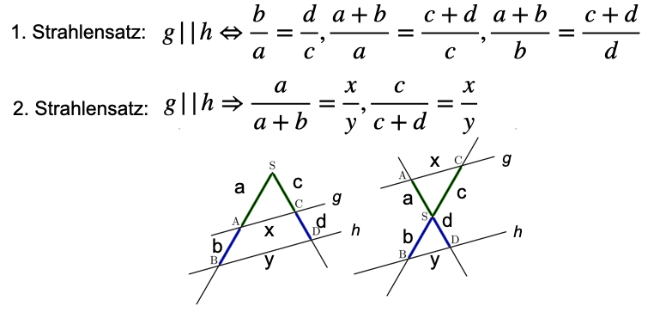
Betrachtet man die beiden Strahlensatzfiguren (V-Figur und X-Figur) genauer, fällt auf, dass die Strahlensatzfiguren aus zwei ähnlichen Dreiecken besteht. Dies demonstriert folgende Aktivität(Autor: Andimoodle) :
Beweis des 1. Strahlensatzes
Da Argumentieren und Beweisen eine Kompetenz ist, die laut Bildungsplan die Schüler*innen erlernen sollen, ist es eine gute Gelegenheit diese Kompetenz zu schulen, indem die Strahlensätze im Unterricht bewiesen werden. Im Folgendem werden 2 Beweisideen aufgezeigt und anschließend werden diese auf Unterrichtstauglichkeit verglichen.
1) vollständige Paktettierung
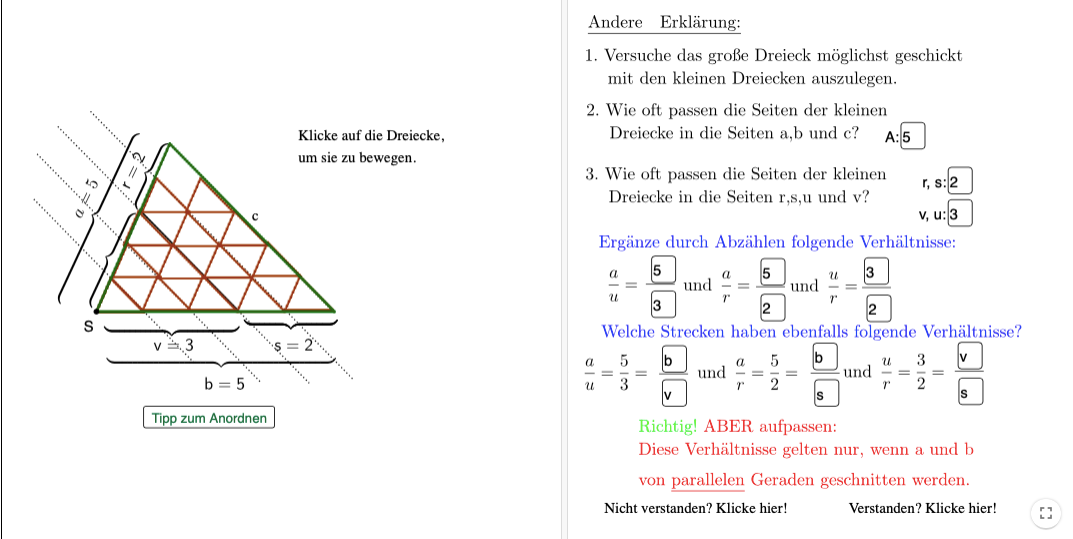
2) Beweis mittels zentrischer Streckung
| vollständige Pakettierung | Beweis mittels zentrischer Streckung |
| - bildliche Herangehensweise, bei der wenig Vorwissen benötigt wird -> gut nachvollziehbar - Beweis oder Herleitung? - Konstruktion vor Instruktion anwendbar | - baut auf Vorhandenem Wissen auf + schafft Verküpfungen -> wer zentrische Streckung nicht verstanden hat, kann den Beweis schwer nachvollziehen - Beweis - SuS lernen Argumentieren und Beweisen |
Umkehrung der Strahlensätze
Wichtig zu wissen ist, dass der 1. Strahlensatz umkehrbar ist und der der 2. Strahlensatz nicht. Um dies zu verdeutlichen bietet es sich an ein Gegenbeispiel für die Umkehrung des 2. Strahlensatzes zu finden und die Umkehrung des 1. Strahlensatzes zu beweisen. Dies wird im folgendem gezeigt:
Gegenbeispiel zur Umkehrung des 2. Strahlensatzes
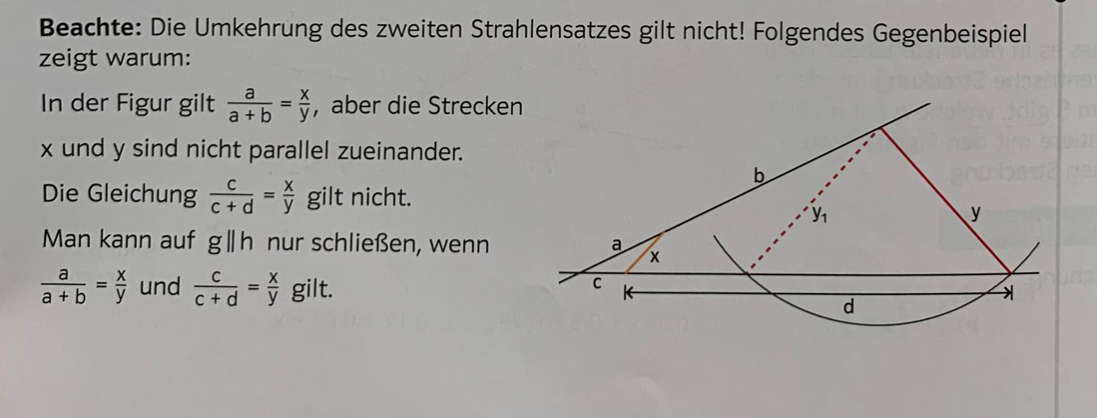
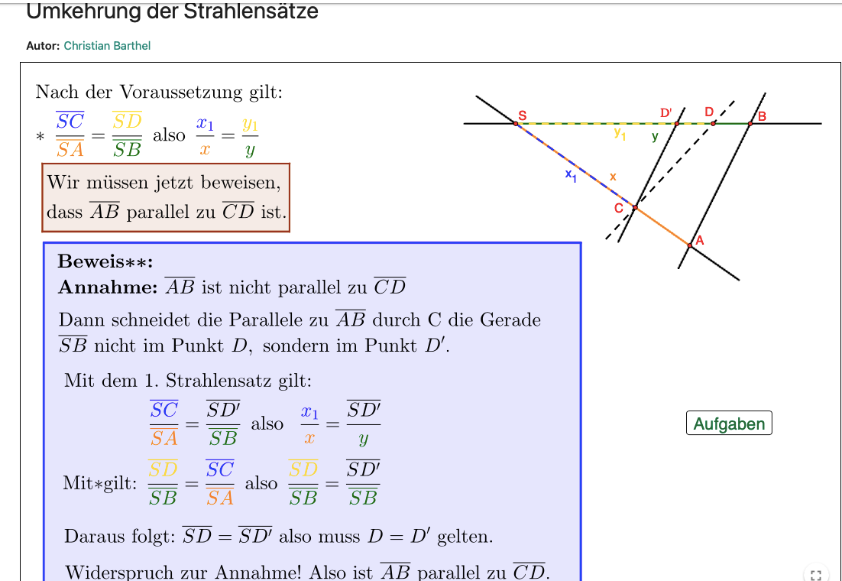
Beweis zur Umkehrung des 1. Strahlensatzes
