kust Groot-Brittannië
- Klik op de knop meet met lengte 2. Je kunt 22 lijnstukjes rondom de kust van Groot-Brittanië leggen.
- Versleep nu de schuifknop en halveer de lengte van de lijnstukjes. Geraak je nu rond met 44 lijnstukjes? Probeer het uit met de knop meet met lengte 1.
Met kortere lijnstukjes kan je beter de onregelmatige kust volgen.
Wanneer je de lengte van de lijnstukjes halveert, heb je meer dan het dubbel aantal lijnstukjes nodig om helemaal rond te geraken.
BenoitMandelbrot boog zich over de vraag: "Hoe lang is de kust van Groot-Brittannië?"
Mandelbrot ontdekte dat de gevonden lengte afhangt van je meeteenheid.
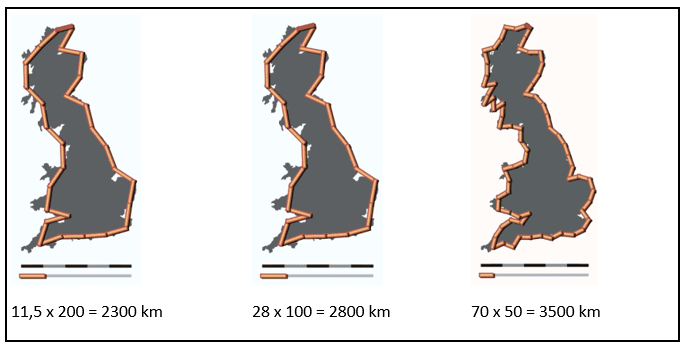
Neem je een meetlat van 200 km, dan kan je heel moeilijk de onregelmatigheden volgen van de kust.
Met een meetlat van 100 km kan dat al beter, met een van 50 km nog beter.
Het lijkt alsof de kustlijn steeds langer wordt. Je zou denken dat je de 'juiste' lengte steeds beter benadert door je meetlat te verfijnen, maar de lengte blijft integendeel onbeperkt toenemen. Ze lijkt oneindig lang, al is ze beperkt. Mandelbrot besloot dat de kustlijn een dimensie moest hebben tussen 1 en 2.
Eigenaardig is dat bij herhaaldelijk inzoomen de verhouding tussen de gemeten lengte en de zoomfactor steeds constant bleef: 1,25. Deze verhouding noemde hij de fractale dimensie van de kustlijn.