Nichttransitivität
Herausforderung
Schritt 1 Das Spiel
Für das Spiel benötigen Sie, einen Partner und drei Efron Bradley Würfel. Die Durchführung folgt den Regeln:
- einer der beiden Spieler beginnt und wählt einen Würfel der drei Würfel aus.
- der zweite Spieler nimmt sich einen der verbleibenden Würfel zwei Würfel.
- beide Spieler würflen gemeinsam, der Würfel mit der höheren Augenzahl gewinnt.
3. Schritt Systematisierung
Tragen Sie die Anzahl der jeweiligen Gewinne in die Tabelle ein.
In der zweiten Tabelle werden dann die realtiven Gewinne angezeigt.
Tabelle zum Eintragen der Ergebnisse
4. Schritt "theoretische Systematisierung"
Ohne Baum gehts kaum! Bestimmen Sie mittels dem Baumdiagramm die einzelnen Gewinnwahrscheinlichkeiten und halten Sie diese auf Ihrem Arbeitsblatt fest.5. Schritt Theoretische Einbindung und Begründung des Themas
Die Wahrscheinlichkeitstheorie hält für uns viele Ergebnisse bereit, die unserer Intention zu wider laufen. Eine dieser überraschenden Ergebnisse sind die hier vorgestellten Würfel.Inititiv gehen wir von folgender Impliaktion aus:
Wenn Hans kleiner als Gretel und Gretel kleiner als Anna ist, dann ist auch Hans kleiner als Anna. In mathematischer Notation.
1. Hans<Gretel Gretel<Anna Hans <Anna
oder:
2. Blei ist schwerer als Wasser und Wasser ist schwerer als Luft, also isz Blei schwerer als Luft.
d.h. die Eigenschaft "geht durch", sie ist transitiv
Nicht so bei den Würfeln, weshalb diese als nichttransitiv bezeichnet werden
Erste Übungen
Übung 1: Das Spiel: Schere, Stein, Papier ...
Übung2: Zum eigenständigen Überprüfen und Festigen
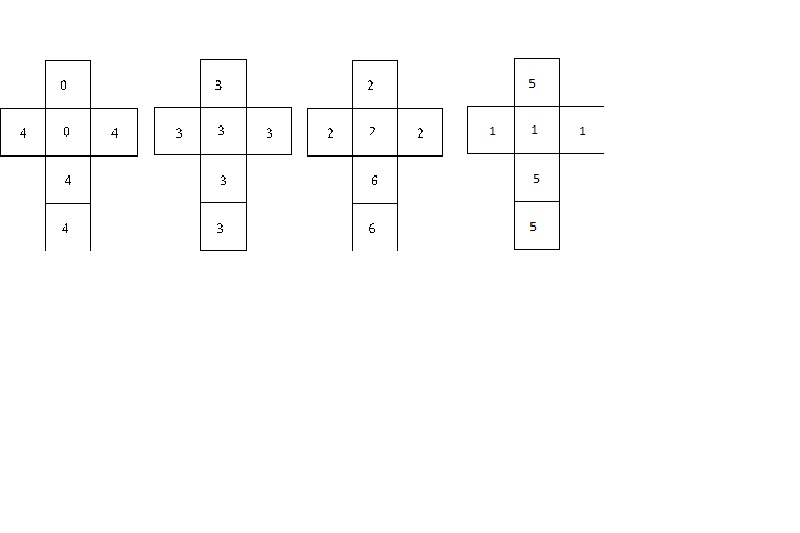
Untersuchen Sie, ob es sich bei den Netzen folgender Würfel um intransitive Würfel handelt und geben Sie gegebenenfalls eine begründete Spielstrategie an.
Achten Sie bitte auf eine exakte Notation.