Die trigonometrischen Funktionen Sinus und Cosinus
Einführung
Bisher haben wir schon den Funktionsbegriff* kennengelernt und nun werden wir die trigonometrischen Funktionen Sinus und Cosinus lernen.
Zuerst erkläre ich, was Sinus Cosinus ist durch ein rechtwinkliges Dreieck mit der pythagoräischen Formel (Anwendung in der Mathematik) danach werde ich sie geometrisch erklären.
Sinus und Kosinus, bezeichnet mit sin(x) und cos(x), sind zwei grundlegende trigonometrische Funktionen, die sie werden ausgehend vom goniometrischen Umfang definiert und ordnen jeder Ecke zu ein gegebenen numerischen Wert zwischen -1 und +1.
Eines der allerersten Ziele der Trigonometrie ist das Studium goniometrischer Funktionen, d.h bestimmter Funktionen, die durch das goniometrische Feld gebildet werden. In dieser Lektion erklären wir, was Sinus und Cosinus eines Winkels bedeuten, schlagen die Definitionen vor und achten besonders auf die grafischen und geometrischen Aspekte der Definitionen.
Darüber hinaus werden wir uns mit den Definitionen von Sinus und Cosinus eines Winkels befassen, seine Haupteigenschaften hervorheben, Amplitude,Frequenz , Phase erklären und einige Beispiele/Aufgabe vorschlagen.
*Definition
(Abbildung). Seien A; B Mengen. Eine Abbildung f von A nach B ist eine Vorschrift, die jedem Element x A genau ein Element y = f(x) 
B zuordnet. Man nennt A den Definitionsbereich und B den Wertebereich von f. Schreibweisen:
B zuordnet. Man nennt A den Definitionsbereich und B den Wertebereich von f. Schreibweisen: f : A ->B, x -> y, oder f : A ->B, f(x) = y.
Man nennt Abbildungen auch Funktionen, vor allem dann, wenn die Werte Zahlen sind (Z, Q,R, C, . . . ).
1.Darstellung und Definition von Sinus und Cosinus
Beginnen wir mit der Definition von Sinus und Cosinus. Betrachten wir einen Winkel auf dem Einheitskreis(), d.h. wir ordnen diesen Winkel () so an, dass sein Scheitel mit dem Mittelpunkt des Umfangs O(0,0) und seine erste Seite mit der positiven Halbachse von x zusammenfällt.( Abbildung 1.1 )
Der fragliche Winkel kann sowohl positiv als auch negativ sein ( Abbildung 1.1 und Abbildung 1.2) und es kann sowohl in Grad als auch in Radiant* ausgedrückt werden.
*Da 2π Radiant 360 ° entspricht, 1π Radiant 180 ° entspricht, π / 2 Radiant 90 ° entspricht usw.
Um einen Winkel von Grad in Bogenmaß umzuwandeln, führen Sie einfach eine einfache Proportion durch. Nennen Sie α einen Winkel in Grad und β einen Winkel im Bogenmaß, wir haben:
α°: β = 180°: π oder β = α°⋅π / 180° oder α °= 180°⋅β / π
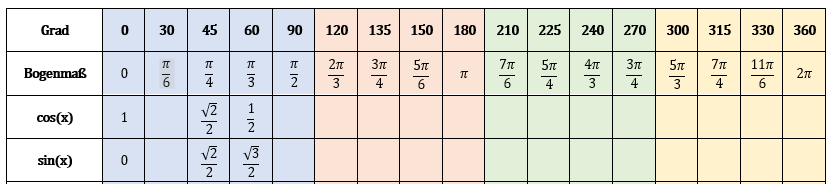
Aufgabe 1.1 : Transformieren Sie die folgenden Winkel von Grad in Bogenmaß und umgekehrt . Versuch mal die Tabelle 1 weiter hinzufügen.Tabelle1.1
Tabelle 1.1_Lösungen
Abbildung 1.1.Winkel entgegen dem Uhrzeigersinn_positiv
Abbildung 1.2. Winkel im Uhrzeigersinn_negativ
Wir nennen P den Punkt, der von der zweiten Seite des Winkels auf dem goniometrischen Umfang geschnitten wird; dieser Punkt wird ein Punkt genannt dem β-Winkel zugeordnet. Dann seien Xp und Yp die Abszisse und Ordinate des Punktes P.( Abbildung 1.3)
Abbildung 1.3. Punkt P(Xp,Yp) ordnet dem ß-Winkel zu
1.2. Definition des Sinus eines Winkels
Bei einem Winkel β auf dem goniometrischen Umfang wird die Ordinate des zu β gehörenden Punktes P als Sinus des Winkels β bezeichnet, dh:
Hinweis:Die Notation OQ überstrichen gibt das vorzeichenbehaftete Maß des OQ-Segments an.
Mit anderen Worten, das Maß ist positiv, wenn dieses Segment auf der positiven Halbachse der Ordinate liegt, negativ, wenn es auf der negativen Halbachse des y liegt.
sin(β) = Yp
Ganz analog lässt sich der Sinus eines Winkels wie folgt definieren: Sei P der einem β-Winkel zugeordnete Punkt auf dem goniometrischen Umfang und sei Q die Projektion des Punktes P auf die y-Achse. Auf diese Weise wird ein rechtwinkliges Dreieck OPQ gebildet, dessen Hypotenuse OP als Radius des goniometrischen Umfangs 1 misst. Der Sinus des Winkels ist das Verhältnis zwischen Kathete OQ und Hypotenuse OP des Dreiecks. (Abbildung 1.4) In Formeln:
Hinweis:Die Notation OQ überstrichen gibt das vorzeichenbehaftete Maß des OQ-Segments an.
Mit anderen Worten, das Maß ist positiv, wenn dieses Segment auf der positiven Halbachse der Ordinate liegt, negativ, wenn es auf der negativen Halbachse des y liegt.Abbildung 1.4. Sinus
1.3. Definition des Cosinus eines Winkels
Bei einem Winkel ß auf dem goniometrischen Umfang ist der Kosinus des Winkels ß die Abszisse des zu ß gehörenden Punktes P, also:
da OP der Radius des goniometrischen Umfangs ist.
Auch in diesem Fall meinen wir mit der Notation OR überstrichen das Maß mit dem Vorzeichen der Kathete OR, das lautet: positiv, wenn dieses Segment auf der positiven Halbachse der Abszisse liegt oder negativ, wenn es auf der negativen Halbachse der Abszisse liegt.
cos(ß)=Xp
Wiederum können wir den Kosinus eines Winkels als das Verhältnis zwischen Kathete OR und Hypotenuse OP des rechtwinkligen Dreiecks OPR definieren, wobei R die Projektion des Punktes P auf der Abszissenachse ist. ( Abbildung 1.5.)
da OP der Radius des goniometrischen Umfangs ist.
Auch in diesem Fall meinen wir mit der Notation OR überstrichen das Maß mit dem Vorzeichen der Kathete OR, das lautet: positiv, wenn dieses Segment auf der positiven Halbachse der Abszisse liegt oder negativ, wenn es auf der negativen Halbachse der Abszisse liegt.
Abbildung 1.5. Cosinus
1.4. Sinus und Cosinus: Vom Einheitskreis zur Funktion
Die Animation, die zeigt, wie die Sinus-Funktion (in rot_roter Punkt D) aus der y-Koordinate eines Punktes B' auf dem Einheitskreis (in grün) im Winkel ß gezeichnet wird.
Im Analog zeigt die Animation ,wie die Kosinus_Funktion (in Blau_blauer Punkt E) aus der x-Koordinate eines Punktes B' auf dem Einheitskreis (in grün) im Winkel ß gezeichnet wird.(Abbildung 1.6.)
Abbildung 1.6. Sinus und Cosinus: Vom Einheitskreis zur Funktion
Wenn man den Radius (Hypotenuse OP) ändert( Winkel bleibt gleichmäßig), variiert verhältnisgleich auch die Kathete OQ und der Sinus Wert und Cosinus Wert ändert nicht. (Abbildung 1.7.)
Abbildung 1.7. Radius ändern
2.Eigenschaften von Sinus und Cosinus
1.Die Kosinus- und Sinus-Funktion sind daher auf R definiert (x R) und sie nehmen alle Werte des
Intervalls -1; 1 an.
und 2.Sie sind periodische Funktionen mit einer minimalen Periode von 2 . Beachten Sie, dass wir die Länge x um 2 vergrößern oder verkleinern, den Umfang jeweils im Uhrzeigersinn oder gegen den Uhrzeigersinn umdrehen und zum gleichen Punkt P (x) zurückkehren. Mit anderen Worten, es gilt der Periodizitätsbericht.
und , für
3.Sie erfüllen die grundlegende trigonometrische Beziehung (Trigonometrischer Pythagoras):, für
Wir einigen uns auf die folgende Notation:, 4.Aus der geometrischen Bedeutung ist ersichtlich, dass die Sinusfunktion ungerade ist, während die Kosinusfunktion gerade ist.und
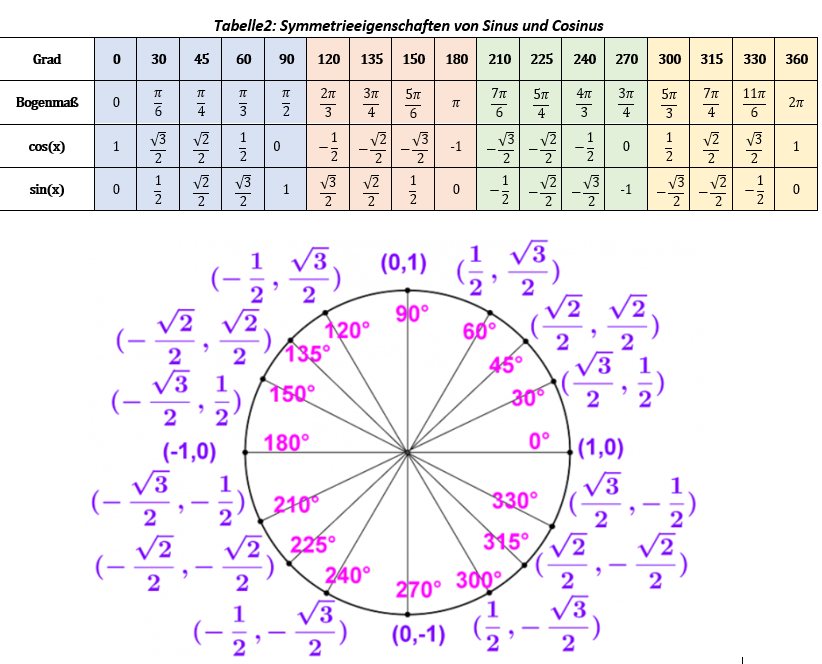
Einige bemerkenswerte Werte der Funktionen sind in der folgenden Tabelle (Tabelle 2.) aufgeführt (wobei k eine beliebige relative ganze Zahl bezeichnet):
Tabelle 2.
Von erheblicher Bedeutung sind die Additions- und Subtraktionsformeln.
Für alle gilt:
,
1.Aus die beiden Additionstheoreme kann man z.B einsetzen :
,
Wie grafisch vermerkt, sehen wir auch aus den Formeln, dass der Graph der Kosinusfunktion aus dem der Sinusfunktion durch eine Linksverschiebung von erhalten wird.
2.Aus ihnen erhalten wir bei entsprechender Themenwahl wie z.B beispielsweise die Verdopplungsformeln:
,
3.Aus die beiden Additionstheoreme kann man z.B einsetzen :
,
2.1. Additionstheoreme und Subtraktionstheoreme
Von erheblicher Bedeutung sind die Additions- und Subtraktionsformeln.
Für alle gilt:
,
1.Aus die beiden Additionstheoreme kann man z.B einsetzen :
,
Wie grafisch vermerkt, sehen wir auch aus den Formeln, dass der Graph der Kosinusfunktion aus dem der Sinusfunktion durch eine Linksverschiebung von erhalten wird.
2.Aus ihnen erhalten wir bei entsprechender Themenwahl wie z.B beispielsweise die Verdopplungsformeln:
,
3.Aus die beiden Additionstheoreme kann man z.B einsetzen :
,
2.2. Symmetrieeigenschaften von Sinus un Cosinus im Einheitskreis
Abbildung 2.1 I Quadrant Komplementärwinkel
II Quadrant: Werte für _Zusätzliche Winkel(Abbildung 2.2)
Zwei Winkel heißen zusätzlich, wenn sie zusammen einen flachen Winkel bilden, zum Beispiel und repräsentieren die Breiten zweier zusätzlicher Winkel. Auf dem goniometrischen Umfang kennzeichnen die End-seiten zweier zusätzlicher Winkel zwei Punkte B' und D, die bezüglich der Ordinatenachse symmetrisch sind. Die Ordinaten sind also gleich, während die Abszissen das entgegengesetzte Vorzeichen haben und somit gilt:
Beachten Sie, dass die Zeichnung in Bezug auf die y-Achse gespiegelt ist und sich daher Sinus und Cosinus nicht vertauschen, sondern der Cosinus negativ wird, da er auf der linken Seite der x-Achse liegt.
Abbildung 2.2. II Quadrant_ Zusätzliche Winkel: y -Achse Symmetrie _Sinus und Cosinus
III Quadrant: Werte für Komplementärwinkel (Abbildung 2.3)
Im dritten Quadranten haben wir die Beziehungen zwischen den Winkeln und : der , also das Segment FG, ist gleich dem Segment FH, das dem entspricht, während der , also ist das Segment FC, entspricht dem, das ist das Segment FE .Sinus und Cosinus tauschen sich in diesem Fall nicht aus, sondern werden beide negativ.
Abbildung 2.3. III Quadrant_Komplementärwinkel
IV Quadrant: Werte für Entgegengesetzte Winkel( und =- )(Abbildung 2.4)
Zwei Winkel sind entgegengesetzt, wenn sie die gleiche Amplitude im Absolutwert, aber unterschiedliche Vorzeichen haben. Auf dem goniometrischen Umfang ist einer im Uhrzeigersinn () und der andere gegen den Uhrzeigersinn() orientiert: Sie sind symmetrisch zur Abszissenachse und daher:
weil die Abszissen unverändert bleiben: Sinus und Kosinus vertauschen sich nicht, aber der Sinus ist negativ.
Abbildung 2.4: IV Quadrant_Entgegengesetzte Winke: x-Achse Symmetrie _Sinus und Cosinus
Aufgabe1:
Nun bist du dran.
Jetzt, da sie alle Informationen wie Sinus und Cosinus in den verschiedenen Quadranten haben, sollten sie in der Lage sein, die folgende Tabelle auszufüllen.
Versuch mal die Tabelle 2.1 weiter hinzufügen.
Hinweise: Für die Symmetrie des goniometrischen Umfangs gibt es Winkelpaare, für die sich die Kosinus- und Sinuswerte leicht voneinander ableiten lassen.
Aufgabe2:
Rechnen sie bitte :
a)
b)
c)
