Criterio de congruencia LLL
Algunas palabras sobre la congruencia de triángulos
¿Alguna vez has escuchado que alguien dice "esa persona es muy congruente"? Cuando se afirma algo así, lo que se está diciendo es que lo que esa persona hace empata perfectamente con lo que dice o piensa. ¿Y eso qué tiene que ver con los triángulos? Pues justamente que a veces nos interesa comprobar si dos triángulos son exactamente iguales o, como dicen los matemáticos, queremos verificar que son congruentes.
Para asegurarnos de que dos triángulos no es suficiente basarnos en lo que nos dice nuestra vista. Veamos el siguiente ejemplo:
¿Son idénticos estos triángulos?
Parece que sí ¿verdad? Veamos si es así. Uno de los criterios de congruencia dice que dos triángulos son idénticos si las medidas de sus lados respectivos son iguales. ¡Qué bobada! Pues claro, si los lados de dos triángulos son iguales por pares, pues es lógico que son igualitos. Pues no es ninguna bobada y, de hecho, ese es el primer criterio de congruencia, conocido como LLL (Lado, Lado, Lado). Para ver si los triángulos que están dibujados arriba, utiliza la herramienta 
y mide cada uno de los segmentos.
y mide cada uno de los segmentos.Y después de medirlos...
¿Son los triángulos ABE y FCD congruentes? ¿Por qué?
Cómo pudimos comprobar, los triángulos no eran congruentes. Ahora mide los lados de los triángulos que aparecen a continuación con la herramienta sin mover ninguno de los puntos.
sin mover ninguno de los puntos.Triángulos congruentes por criterio LLL
¿Son estos triángulos congruentes?
¡A moverse!
Ahora vamos a ver qué sucede si movemos los vértices de los triángulos. Selecciona con la herramienta 
cualquiera de los vértices que aparecen en color morado y muévelo. ¿Qué esperaríamos que suceda con las medidas de los lados de los triángulos si estos son congruentes? Repite esta operación con los demás vértices.
cualquiera de los vértices que aparecen en color morado y muévelo. ¿Qué esperaríamos que suceda con las medidas de los lados de los triángulos si estos son congruentes? Repite esta operación con los demás vértices.¿Son congruentes los triángulos aún moviendo los vértices? Justifica tu respuesta.
Las rayitas que se colocan en los lados de los triángulos de abajo simbolizan que los triángulos son congruentes por el criterio LLL
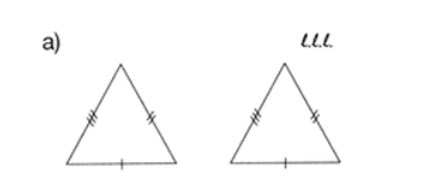
¡Ahora te toca a ti!
Es momento de poner manos a la obra. Observa la figura de abajo. Ahora construye un triángulo congruente al triángulo ABC teniendo en mente el criterio LLL. Para tener un punto de partida, hemos colocado uno de los lados de ese triángulo (obviamente respetando su medida). Sugerencia: utiliza la herramienta Compás 
para realizar esta tarea. Luego arrastra los vértices morados de cualquiera de los triángulos y usa la herramienta Distancia para validar tu construcción.
para realizar esta tarea. Luego arrastra los vértices morados de cualquiera de los triángulos y usa la herramienta Distancia para validar tu construcción.Algunas palabras sobre la congruencia de triángulos
¿Alguna vez has escuchado que alguien dice "esa persona es muy congruente"? Cuando se afirma algo así, lo que se está diciendo es que lo que esa persona hace empata perfectamente con lo que dice o piensa. ¿Y eso qué tiene que ver con los triángulos? Pues justamente que a veces nos interesa comprobar si dos triángulos son exactamente iguales o, como dicen los matemáticos, queremos verificar que son congruentes.
Para asegurarnos de que dos triángulos no es suficiente basarnos en lo que nos dice nuestra vista. Veamos el siguiente ejemplo:
Algunas palabras sobre la congruencia de triángulos
¿Alguna vez has escuchado que alguien dice "esa persona es muy congruente"? Cuando se afirma algo así, lo que se está diciendo es que lo que esa persona hace empata perfectamente con lo que dice o piensa. ¿Y eso qué tiene que ver con los triángulos? Pues justamente que a veces nos interesa comprobar si dos triángulos son exactamente iguales o, como dicen los matemáticos, queremos verificar que son congruentes.
Para asegurarnos de que dos triángulos no es suficiente basarnos en lo que nos dice nuestra vista. Veamos el siguiente ejemplo:
¿Alguna vez has escuchado que alguien dice "esa persona es muy congruente"? Cuando se afirma algo así, lo que se está diciendo es que lo que esa persona hace empata perfectamente con lo que dice o piensa. ¿Y eso qué tiene que ver con los triángulos? Pues justamente que a veces nos interesa comprobar si dos triángulos son exactamente iguales o, como dicen los matemáticos, queremos verificar que son congruentes.
Para asegurarnos de que dos triángulos no es suficiente basarnos en lo que nos dice nuestra vista. Veamos el siguiente ejemplo: