Aspectos generales
Reto 1A. Circunferencias tangentes
A partir de dos circunferencias construye la circunferencia que sea tangente a ambas circunferencias.
¿Es única?
En una primera construcción vamos a construir las cincunferencias tangentes interior y exterior a dos circunferencias dadas.
Los pasos que hay que realizar, una vez dibujadas las dos circunferencias, será trazar la recta que pasa por lo centros de ambas circunferencias.
A continuación se obtienen los puntos de intersección con las dos circunferencias.
Si los puntos de interseccion con la primera circunferencia son E y F, y con la segunda son G y H, las cicunferencias tangentes tendrán como centro el punto medio del segmento EH y la segunda tendrá el centro en el punto medio del segmento FG, tal y como aparece en el applets mostrado a continuación.
Como se han construido dos circunferencias ya tenemos la respuesta a la pregunta, la circunferencia tangente no es única.
Circunferencias tangentes
Esta actividades ofrece muchas posibilidades para construir las infinitas circunferencias tangentes que existen.
A continuación incluimos dos construcciones distintas, enviadas por los participantes del club, en las que aparecen infinitas circunferencias.
Infinitas circunferencias tangentes
En la construcción anterior, tal como indica el autor, hay infinitas soluciones. Existe una circunferencia tangente siempre que , con igual a la amplitud del ángulo EFC.
Dadas las enormes posibilidades que este reto ofrece, recomendamos leer el siguiente artículo:
Tangent Circles of Two Separate Circles escrito porBrian Swanagan, publicado en The University of Georgia, diponible en la direccón:
http://jwilson.coe.uga.edu/EMAT6680Su06/Swanagan/Assignment7/BSAssignment7.html
Reto 2A. Rectángulo y triángulo de igual área
A partir de un rectángulo cualquiera, previamente creado de manera que al mover sus elementos siga manteniendo la condición de rectángulo, construye un triángulo cuya área sea igual a la del rectángulo inicial.
Dado un rectángulo de base b y altura a, se trata de construir un triángulo que tenga el mismo área, es decir a.b
Por tanto como el área del triángulo es un medio del producto de la base por la altura del triángulo, para que se cumpla la condición pedida, bastará con realizar una de las dos siguientes construcciones:
a. Construir un triángulo que tenga doble base que el rectángulo y la misma altura.
b. Construir un triángulo que tenga igual base y doble altura que el triángulo.
En el primer caso, se pueden realizar los pasos siguientes:
1. Trazamos la recta sobre la base del triángulo, con ayuda de la herramienta Circunferencia, se traza una circunferencia de radio igual a la base del rectángulo. El punto de intersección con la recta nos dará el diámetro y por tanto, será el doble de la base.
2. Trazamos la recta que pasa por los vértices de la base opuesta del rectángulo.
3 Cualquier punto situado en esta recta será el tercer vértice del triángulo buscado.
Realizamos esta construcción en el applets mostrado a continuación.
Hay que tener en cuenta que el rectángulo se deberá construir de manera que al mover sus vértices, mantenga sus propiedades.
En el applet siguiente al mover F se obtienen infinitos triángulos con igual área que el rectángulo.
Rectángulo y triángulo de cualquier área
De igual manera se construye el segundo caso en el que se mantiene la base del rectángulo y se hace doble la altura.
Mostramos a continuación una nueva construcción en la que hemos realizado una animación.
Reto 1B. Triángulo en movimiento
Construye un triángulo cuyos vértices sean el centro de la circunferencia y dos puntos sobre ella, de manera similar a como aparece en la imagen, de manera que al animar el punto C, el triángulo gire sobre la circunferencia sin deformarse.
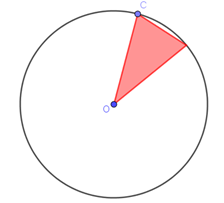
El primer objeto que se debe contruir es la circunferencia, situando un punto C sobre ella. Este punto debe ser distinto del utilizado para crear la circunferencia con la herramienta Circunferencia (centro-punto).
A continuación con centro en C se traza una nueva circunferencia con la herramienta Circunferencia (centro-radio). El radio puede ser cualquier valor, por ejemplo una unidad para que al mover C el triángulo que vamos a crear no se deforme.
El siguiente paso será obtener los puntos de intersección entre las dos circunferencias.
Y por último, solo queda crear el triángulo cuyos vértices serán el centro O de la primera circunferencia, el punto C y uno de los dos puntos de intersección de las dos circunferencias.
Ya solo queda mover C o activar su animación para comprobar el movimiento del triángulo que no se desformará.
Una vez ocultados todos los objetos, dejamos solo la circunferencia inicial, el punto C y el triángulo que se moverá al aplicar movimiento al punto C.
Reto 2B. Relación entre áreas de polígonos
Dibuja con GeoGebra un polígono de tres lados. Traza sus puntos medios y únelos. Determina la razón o proporción entre las áreas del segundo triángulo y del primero. ¿Qué resultado puedes conjeturar?
Mueve los vértices del triángulo original y comprueba si tu conjetura sigue siendo válida.
Por semejanza entre los triángulos, las longitudes de los tres lados del triángulo interior son la mitad de las de sus correspondientes en el triángulo inicial. Así pues, se tratará de figuras semejantes con razón de semejanza igual a 1/2. Por consiguiente, las razones entre las áreas será el cuadrado de 1/2, o sea 1/4.
Dibuja ahora un cuadrilátero y traza sus puntos medios. Únelos. Determina la razón o proporción entre las
áreas del segundo polígono obtenido y del primero. ¿Qué resultado puedes conjeturar?
Mueve los vértices del cuadrilátero original y comprueba si tu conjetura sigue siendo válida.
La relaciónanterior está determinada por el teorema de Varignon que determina que al unir los puntos medios de un cuadrilátero, el polígono obtenido es un paralelogramo y su área es la mitad del área del cuadrilátero inicial.
Comprobemos qué ocurre con un polìgono de 5 lados y con uno de seis.