1. Verschieben von Funktionsgraphen
Mittlerweile kennst du schon sehr viele Funktionsklassen: ganzrationale Funktionen, Exponentialfunktion, Wurzelfunktion, trigonometrische Funktionen,...
Über einzelne Graphen, wie von Parabeln oder trigonometrischen Funktionen, kannst du schon sehr detaillierte Aussagen treffen. Du weißt wie sie zusammenhängen oder wo Hoch- und Tiefpunkte sind. In diesem Kapitel betrachten wir Funktionsgraphen ganz allgemein, sodass wir nicht mehr so sehr abhängig vom Wissen über die jeweilige Funktionsklasse sind.
Wir beginnen mit der Verschiebung von Graphen.
Wiederhole in folgender LearningApp, was du noch über die Verschiebung von Parabeln weißt.
Auch über die allgemeine Sinusfunktion hast du schon einiges gelernt.
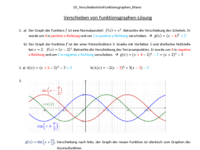
Erinnerung:
f(x) = a sin (b(x+c)) + d
a: Streckung in y-Richtung
b: Streckung in x-Richtung
c: Verschiebung an der x-Achse
d: Verschiebung an der y-Achse
Erprobe dein Wissen in folgender LearningApp.
Das, was du über diese speziellen Funktionen schon weißt, wollen wir nun auf allgemeine Funktionen übertragen. Heute beschäftigen wir uns dabei nur mit der Verschiebung.
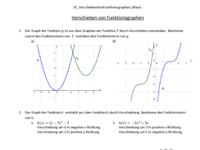
Der Graph von g(x) entsteht aus dem Graph von f(x) durch Verschiebung. Mit dem Schieberegler a kannst du verschiedene Verschiebungen austesten.
Beschreibe in eigenen Worten, wie Der Graph von g verschoben wird und wie sich das im Term g(x) widerspiegelt.
Dann bleibt uns nur noch eine andere Verschiebungsrichtung. Untersuche diese im nächsten GeoGebra-Applet.
Beschreibe, wo sich die Verschiebung im Term erkennen lässt.
Das ganze wollen wir nun im Hefteintrag festhalten.
Erklärvideo

Verständnisfragen
entstand aus durch Verschiebung. Wie wurde verschoben?
entstand aus durch Verschiebung. Wie wurde verschoben?
entstand aus durch Verschiebung. Wie wurde verschoben?
entstand aus durch Verschiebung. Wie wurde verschoben? Tipp: Betrachte ganz genau, was gerechnet wurde.
Und jetzt wird geübt.
Die folgenden Übung findest du im...
Buch S. 129
Tipp: Suche die markante Punkte, wie Nullstellen, Hoch- oder Tiefpunkte und betrachte, wie sie verschoben wurden.
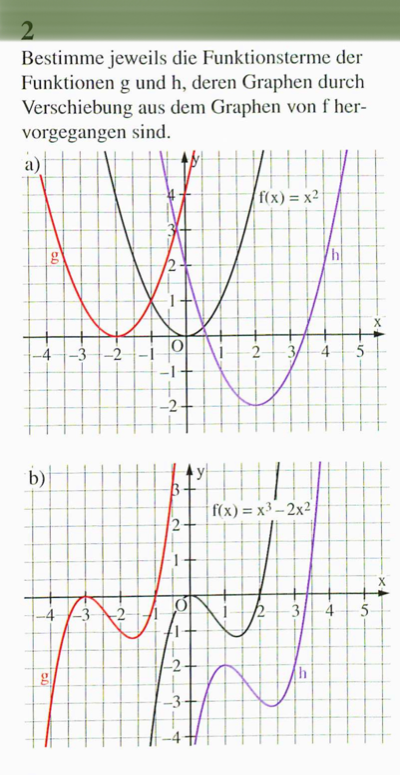
Lösung a)
Lösung b)
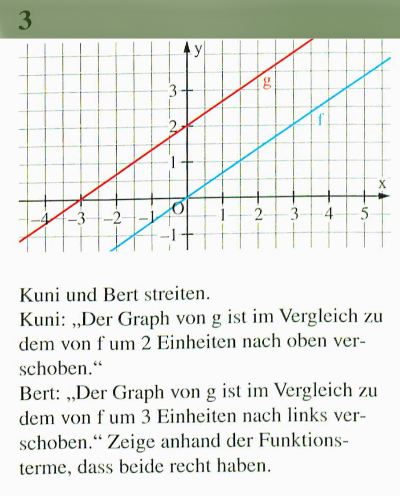
Lösung

Lösung
Löse jetzt noch das folgende Arbeitsblatt. Aufgabe 3 ist dabei freiwillig.
Die Lösung findest du darunter.