Applet. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Let there be some distribution created by discrete set of points in a Euclidean space. Consider two estimators of location of this distribution:
the geometric median (GM) -the point minimizing the sum of distances to the all points and
the geometric center (GC), defined as point minimizing the sum of the squares of the distances to each point.
We generalize these estimates to the case when they are searched in a restricted region, for example, finding these estimates on a circle of radius R.
lP:={p1,p2,p3,p4,p5,p6} -discrete sample of movable points in the x-y plane.
f(x) =Sum(Zip(sqrt((R* cos(x) - x(b))² + (R* sin(x) - y(b))²), b, lP))}
fq(x) = Sum(Zip(( (R* cos(x) - x(b))² + (R* sin(x) - y(b))², b, lP)).
Functions: f(x) -Sum of distances, fq(x) -Sum of the squares of distances between a set of points lP and a Test Point x0=(R; x) on a circle c.
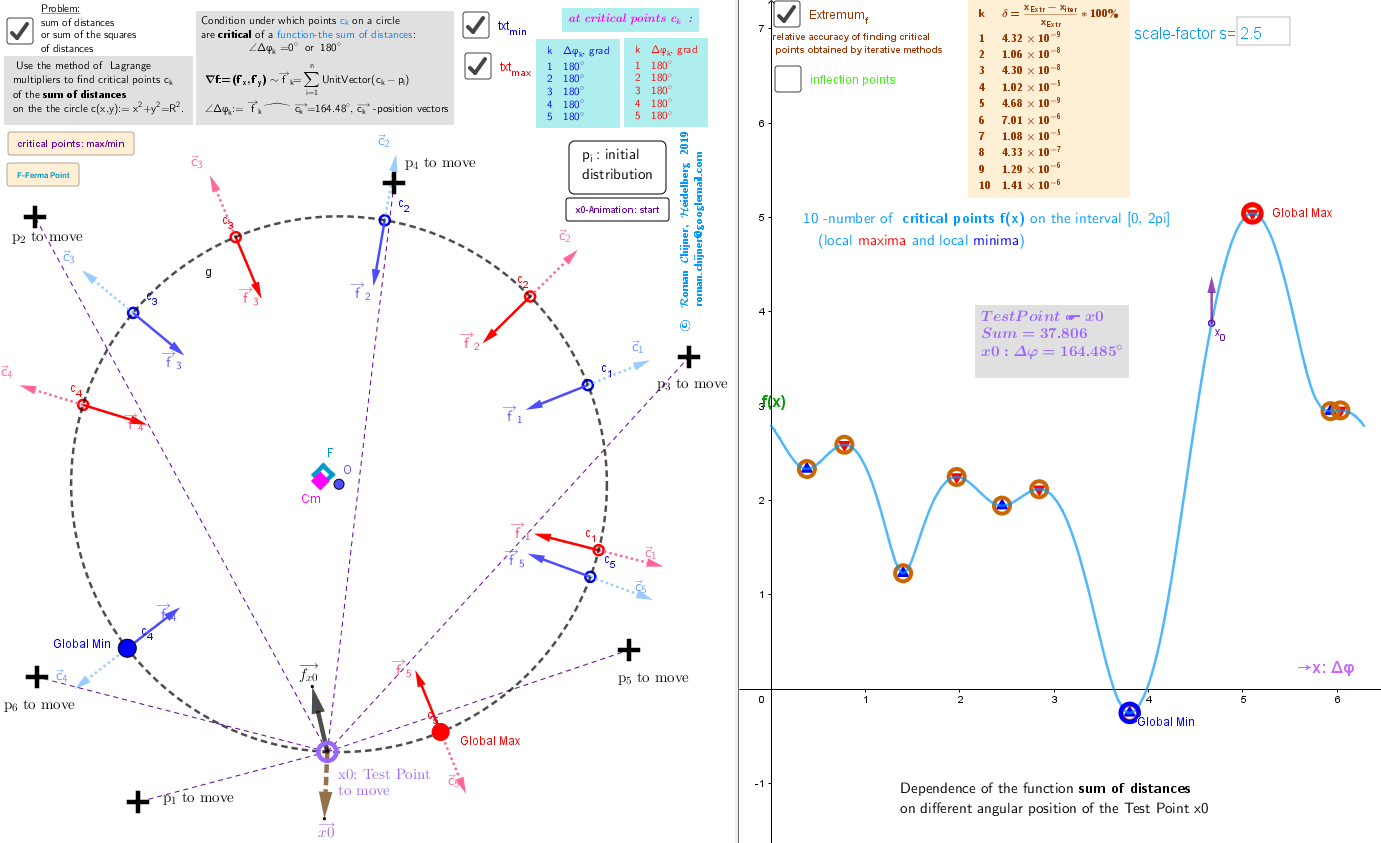
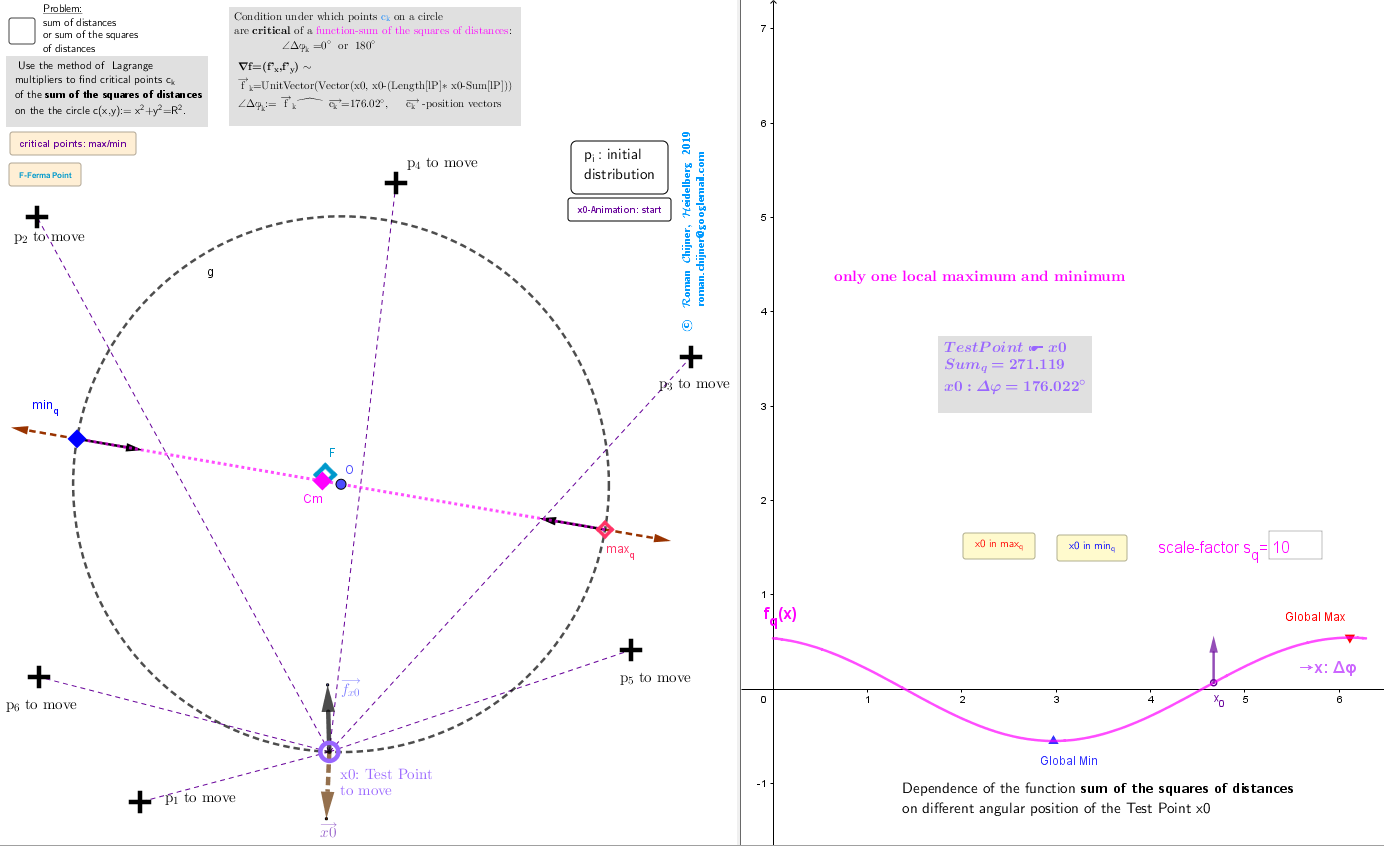
Problem: use the method of Lagrange multipliers to find critical points {ck} of these functions on the the circle c(x,y):= x2+y2=R2.
☛ For illustration: the vectors are attached at points ck.
This applet is used to explore the distribution of geometric medians and centers on the circle of radius R, „induces“ by the discrete sample of movable points from lP in the x-y plane.
Description in https://www.geogebra.org/m/puqnepmv.
In applet: F -Ferma Point; Cm- Centroid.
Some conclusions:
In the case of the Lagrange problem -extremizing the sum of distances from sample points lP to points on the circle, there are exact solutions and iterative solutions -button: critical points: max/min. The results coincide with a high degree. In the Extremumf table, you can see the relative deviation of errors.
By changing the location of points from the lP set, you can verify the validity of the above conclusions. I used these iterative methods for the case of a more complex problem -finding extreme points on a sphere.
In the future, the critical points: local maxima and minima, and saddle points will be called geometric medians of points from lP in a restricted region -circle.
In the case of the Lagrange problem -extremizing of the sum of the squares of the distances, you can find explicit formulas - its coordinates are associated with the average values of the coordinates of points. In this case, the problem has only two critical points -two antipodal points: the local maximum and minimum. This points are on the same axis passing through the center of the circle O and the center of mass Cm and will be called geometric centers of points from lP in a restricted region -circle .
Geometric Medians on the circle
Geometric Centers on the circle
Applets in a book:
Description. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Applet. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Finding the location of geometric medians on the circle of discrete sample points depending on the position of the test point.
Method of Lagrange multipliers. Relative positioning of repulsive movable points on a circle.
Generating an extreme arrangements of points on a circle
Generating an extreme arrangements of points on a sphere
Generating an extreme arrangements of points on a sphere with more structured calculation program-GeoGebra Forum-
https://help.geogebra.org/topic/geogebra-windows-portable-zip-for-december
Iterative methods for optimization -button: critical points: max/min
ltest2 = Sequence((R; 2π / na j), j, 0, na ) -Starting points for iterative methods
lZmax=CopyFreeObject(Zip(Last[IterationList((0,0)+R UnitVector(Sum[Zip(UnitVector(Z1 - r), r, lP)]), Z1, {a}, 300),1 ],a, ltest2))
lZmax' = CopyFreeObject(Unique(Zip((R; round(Angle(a), 16)), a, Flatten(lZmax))) )
lZmin=CopyFreeObject(Zip[Last[IterationList((0,0 )+ R UnitVector[ Sum[Zip[(p/ Length(p - Z2)),p,lP ]] ] , Z2, {a}, 300),1 ],a, ltest2])
lZmin' = CopyFreeObject(Unique(Zip((R; round(Angle(a), 16)), a, Flatten(lZmin))) )