L’équation quotient
Dans cette activité, vous allez explorer la définition, Exemple, propriétés et des Méthodes pour résoudre une équation quotient
Définition :
Toute équation du type où et sont des expressions
algébriques (), est appelée équation-quotient.
Théorème :
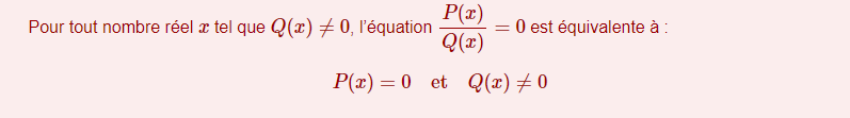
Méthode pour résoudre une équation quotient
La résolution d’équations contenant des quotients se fait selon les étapes suivantes :
Etape n°1 : Identifier toutes les valeurs interdites en analysant les dénominateurs.
Etape n°2 : Regrouper tous les termes à gauche de l’équation pour obtenir une équation nulle.
Etape n°3 : Mettre tous les termes sous le même dénominateur en vue d’obtenir qu’une seule fraction. On obtient alors une équation de la forme
Etape n°4 : Utiliser le théorème du quotient nul et résoudre
Etape n°5 : Vérifier que les solutions trouvées appartiennent à l’ensemble de définition de l’équation.
Etape n°6 : Conclure sur les solutions.
Appliquons ces étapes pour résoudre dans l'équation suivante:
ETAPE N°1 :Identifier la ou les valeur(s) interdite(s)
On commence par identifier la ou les valeur(s) interdite(s) éventuelle(s), c'est-à-dire les valeurs qui annulent le(s) dénominateur(s).
Application : On identifie la ou les valeur(s) interdite(s). Pour tout réel x :
on a
donc x = 1
On en déduit que l'équation n'est pas définie en x= 1. On la résout donc sur .
ETAPE N°2 : Passer tous les termes du même côté de l'égalité
Si l'équation n'est pas une équation quotient nul, on passe tous les termes du même côté de l'égalité.
Application : On passe tous les termes du même côté de l'égalité. Pour tout réel :
on a
donc
ETAPE N°3 : Mettre les fractions sur le même dénominateur
Si l'équation n'est pas un quotient nul, on met ensuite tous les termes sur le même dénominateur.
On obtient une équation quotient nul.
Application : On met tous les termes sur le même dénominateur.
On remarque que , on choisit donc comme dénominateur commun.
Ainsi, pour tout réel :
on a
donc
donc
alors
ETAPE N°4 : Réciter le cours
On récite la propriété : "un quotient est nul si et seulement si son numérateur est nul". On peut alors
transformer l'équation.
Application : Pour tout réel
on a
donc
ETAPE N°5: Résoudre l'équation
On résout l'équation obtenue.
Application : On résout donc l'équation pour tout réel
on a
donc
d'où x =
alors x =-1
ETAPE N°6: Vérifier l'appartenance des solutions au domaine de définition de l'équation et conclure
On vérifie que les solutions obtenues appartiennent bien au domaine de définition de l'équation.
On en déduit les solutions de l'équation quotient.
Application : L'équation est définie sur
Or
On en déduit que l'ensemble des solutions de l'équation est :