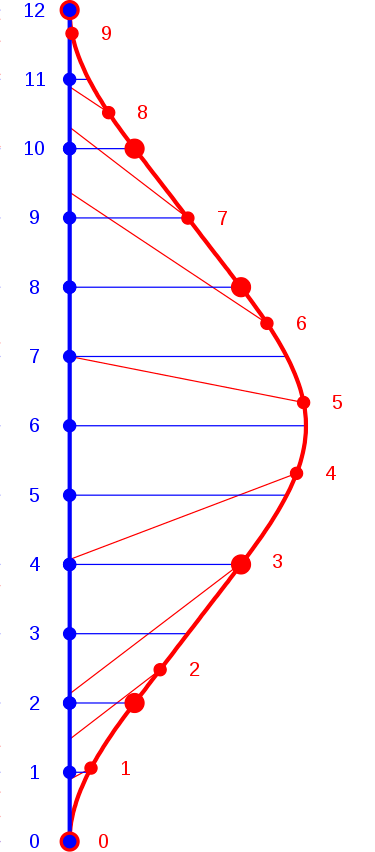
Paradosso dei gemelli
Si consiglia la lettura del testo divulgativo di E. Fabri
http://www.sagredo.eu/divulgazione/relgem/relgem1.htm
Da cui estraggo
"La confutazione più comune [del "paradosso"] è la seguente: se è vero che B si è mosso rispetto ad A, e si spiega che segni un tempo minore per il fatto che si è mosso, basta mettersi dal punto di vista di B per capovolgere l'argomento. Ora B appare fermo ed è A che si allontana e ritorna. Dunque dovrebbe essere A a segnare un tempo minore. Poiché le due cose non possono essere entrambe vere, l'unica via d'uscita è che siano entrambe false, ossia che i due tempi siano uguali.
Si vede che la confutazione si basa su un'idea: che il moto è relativo, e quindi tutti gli effetti del moto debbono essere altrettanto relativi. È notevole che a chi ragiona così può sembrare che la relatività "si dia la zappa sui piedi", perché è proprio uno dei fondamenti della relatività che a tutti gli effetti il moto deve essere considerato relativo, in quanto non esiste un sistema di riferimento privilegiato.
Ma è facile ribattere: la RR asserisce l'equivalenza fra riferimenti inerziali. Ora non è possibile che entrambe le astronavi siano riferimenti inerziali: può esserlo una, o nessuna delle due, ma non entrambe. Dunque la supposta equivalenza non sussiste."
(...)
"Ma è vero allora che il paradosso dei gemelli è un problema di RG? La mia risposta è no, per due ragioni."
(...)
" In particolare si dimostra che questa "lunghezza" [dell'intervallo spaziotemporale] ha una proprietà particolare: fra tutte le curve che uniscono due punti nello spazio-tempo, il segmento di retta ha la lunghezza massima (non minima, ed è per questo motivo che avevo scritto "lunghezza" tra virgolette).
Poiché questa lunghezza non è che il tempo segnato dall'orologio, si vede subito che l'orologio A, che si muove di moto rettilineo uniforme (per cui la sua curva nello spazio-tempo è una retta) segnerà il tempo più lungo rispetto a qualunque altro. E così il paradosso dei gemelli scompare."
---
Selleri la spiega così:
"Dunque il moto rettilineo uniforme è quello a cui corrisponde il tempo proprio maggiore. Dato che, per arrivare comunque al punto finale (spazio e tempo), si dovrà tenere una velocità media identica a quella del percorso di moto uniforme, cambiare velocità durante il tragitto implica assumere anche velocità maggiori della media e in tali tratti il fluire del tempo rallenta più di quanto non acceleri negli eventuali tratti a velocità minori della media: l'effetto finale è di un tempo proprio minore. E diciamo eventuali tratti a velocità minori della media perché potrebbero anche non esserci: si potrebbero tenere velocità sempre superiori alla media invertendone la direzione. Il caso limite è quello di un raggio di luce: viaggiando sempre a c, le sue linee di universo sono sempre inclinate di 45° in ogni sistema di riferimento inerziale (invarianza di c). Due qualsiasi punti di un percorso reale possono sempre essere congiunti con una spezzata costituita da soli tratti a 45° (normalmente a zig-zag). Il tempo proprio di una tale linea di universo (raggi di luce) è sempre nullo. I fotoni infatti arrivano sempre - secondo i loro orologi - nello stesso istante in cui sono partiti" (La Natura del tempo)
https://www.geogebra.org/material/edit/id/qnh59yx6 Asimmetrie nella rilevazione di posizioni e tempi
Sulla Relatività ristretta
SRCalc (Calcolatrice Relatività ristretta)
https://www.geogebra.org/m/wqf5bEum (due piani affiancati)
https://www.geogebra.org/m/XNzUyQcp (unico piano)
https://www.geogebra.org/m/pcUU2s7Q (regolo relativistico) (composizione velocità)
https://www.geogebra.org/m/N2Rybc85 (orologio a luce e calcolo di gamma)
https://www.geogebra.org/m/qnh59yx6 ("paradosso" dei gemelli) ** questo foglio ***
https://www.geogebra.org/m/tahy8kqj (sfere di luce)
Twin paradox From Wikipedia, the free encyclopedia