Hipérbola.
La hipérbola puede definirse como: el lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos llamados focos es constante.
Dicha constante resulta ser la longitud del eje transverso de la hipérbola.
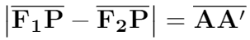
A continuación se muestran y explican cada uno de los elementos de la hipérbola.
Los puntos F1 y F2 son los focos, (mencionados anteriormente en la definición de la hipérbola como lugar geométrico).
El segmento F1F2 se llama distancia focal y su longitud es 2c.
C es el centro, punto medio entre los focos.
Los segmentos F1C y F2C se llama semidistancia focal y su longitud es c.
La recta que pasa por los focos se llama eje focal, y la recta perpendicular a esta y que pasa por C se llama eje secundario.
Si el eje focal es paralelo al eje x, (como el del ejemplo), decimos que la hipérbola es horizontal; en cambio, si es paralelo al eje y, decimos que es vertical.
Las rectas m y n son asíntotas a la hipérbola. Rectas a las cuales la curva se acerca en el infinito pero nunca intercepta.
El círculo con centro C y radio c lo llamaremos círculo focal.
La cuerda que pasa por algún foco (F1 o F2) y es perpendicular al eje focal se llama lado recto.
Los puntos A y A' son los vértices de la hipérbola. Puntos donde el eje focal intercepta a la hipérbola.
El segmento AA' se llama eje transverso y su longitud es 2a.
Los segmentos AC y A'C son semiejes transversos, la longitud de cada uno es a.
Los puntos B y B' son los extremos del eje conjugado.
El segmento BB' es dicho eje conjugado y su longitud es 2b.
Los segmentos BC y B'C son semiejes conjugados, la longitud de cada uno es b.