Tableau de variation d'une fonction
Afin de résumer l'ensemble des variations d'une fonction, nous allons construire un tableau dans lequel nous allons placer des flèches vers le haut (de la gauche vers le droite et du bas vers le haut) sur les intervalles où la fonction est croissante et des flèches vers le bas (de la gauche vers le droite et du haut vers le bas) sur les intervalles où la fonction est décroissante.
Nous appellerons ce tableau le tableau de variation de la fonction.
Dans l'exemple suivant, suivez l'évolution de la construction du tableau de variations de la fonction définie sur [-1;6] en déplaçant le curseur :
Sur ce tableau on voit que la fonction est croissante sur :
Application n°1:
Observer l'évolution du tableau de variations en fonction de l'allure de la courbe en déplaçant les 5 points repérés sur la courbe.
- Faire en sorte que la fonction soit croissante sur [-5;5] puis décroissante sur [5;15] avec un maximum de 8 et un minimum de -2.
Application n°2 :
On considère la fonction définie sur [-3;6] et représentée dans un repère par la courbe Cf suivante :
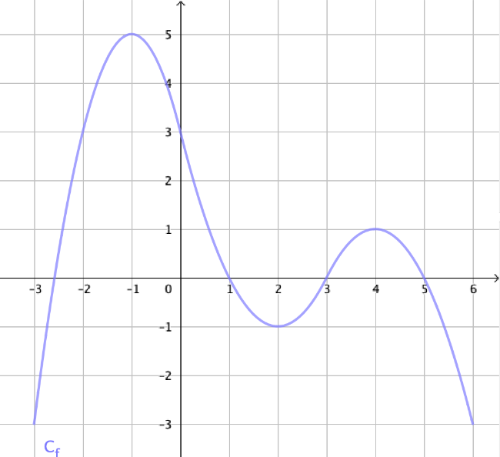
On a construit partiellement le tableau de variation de :
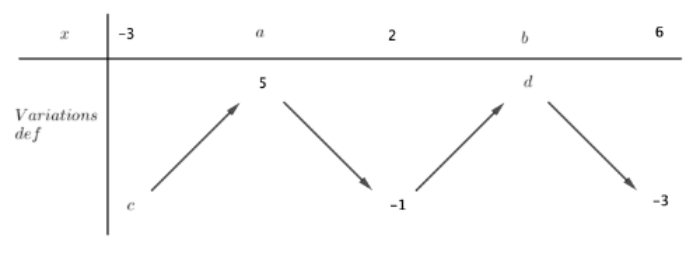
Dans le tableau de variation, quelle est la valeur de ?
Select all that apply
- A
- B
- C
Dans le tableau de variation, quelle est la valeur de ?
Select all that apply
- A
- B
- C
Application n°3 :
On s'intéresse à présent à une la fonction définie sur [-2;5] et dont le tableau de variations est le suivant :
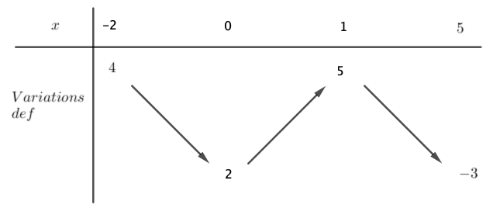
Tracer dans le repère à l'aide de l'outil croquis 
une courbe cohérente avec le tableau de variation de après avoir placé les quatre points imposés par lesquels passe la courbe.
une courbe cohérente avec le tableau de variation de après avoir placé les quatre points imposés par lesquels passe la courbe.Application n°3 :
On considère à présent la fonction définie sur [ ; ] et représentée graphiquement par dans le repère suivant :
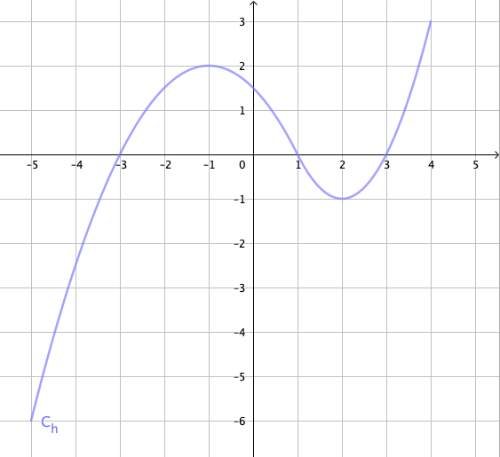
Construire le tableau de variations de à l'aide des différents éléments disponibles par glisser / déposer (tous ne sont pas nécessaires).