원을 접어 정칠각형 만들기 (2) (Folding Heptagon by using Circle paper) - (2)
종이접기 작가 : Philip Chapman-Bell
인터넷 유저 네임 : Oschene
홈페이지: http://origami.oschene.com
Flickr : Philip Chapman-Bell | Flick
Philip Chapman-Bell의 방법을 살펴보자.
정칠각형 접기 바로가기 : Heptagon from a Circle (oschene.com)
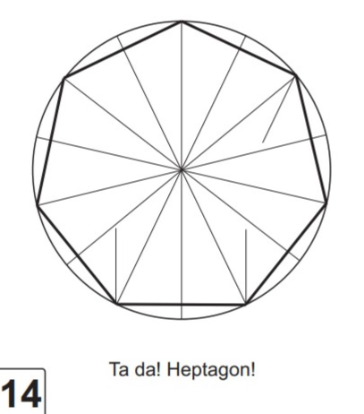
그는 정칠각형, 중심과 꼭짓점을 잇는 중선 7개를 접도록 고안하였다.
그의 방법에서 정칠각형을 접는 부분만 남겨놓으면 아래와 같다.
[질문] 그의 방법으로 접은 것은 정말 정칠각형이 맞을까?
[활동] 어떤 답이 정답일지 방금 접은 정칠각형을 확대해서 확인해봅시다.
아래 그림은 를 한변으로 하는 정칠각형을 정확히 작도한 것입니다.
[정리]
단계가 더 짧은 Oschene (Philip Chapman-Bell)의 방법은 원모양 종이로 정칠각형을 잘 접을 수 있습니다. 하지만 수학적으로는 원의 내접하는 정칠각형보다는 조금 작은 정칠각형을 접은 것입니다.
이것은 정칠각형을 접기 위해 필요한 값 을 구하지 못하고, 그 근사값을 사용했기 때문입니다.
을 구하기 위해서는 3차방정식을 해결해야 합니다.
하지만 Oschene의 방법에 사용한 접기는 [두 점을 지나는 선 접기], [각의 이등분선 접기], [수직이등분선 접기] 뿐이어서, 3차방정식의 해를 구할 수 없습니다.
<비교하기>
원을 접어서 정칠각형을 만들기 : 원을 접어 정칠각형 만들기 (Folding Heptagon by using Circle Paper) – GeoGebra
<추가자료>
를 구하는 방법과 그것을 종이접기로 구현하는 방법은 조에쓰 교육대학에서 이루어진 한 공개강좌의 원고(번역본 링크)를 참고하세요.
조금 요약하면 라 할때,
을 변형하여 을 만들고
로 놓아 식을 한번 더 변형하면 이 됩니다.
이때 이 방정식의 근은 가 됩니다.
종이접기에선 3차방정식의 해를 [종이접기의 공리 6 - 서로 다른 두 점p1, p2과 두 직선l1, l2이 각각 있을 때, 점 p1을 직선 l1 위로, 점 p2를 직선 l2 위로 각각 옮겨지도록 접을 수 있다.]를 이용해서 구할 수 있습니다.