La regla de Sarrus
Para calcular un determinante 3x3 hay que sumar 6 productos. Cada producto es el resultado de multiplicar tres elementos de la matriz, con la condición de que ninguno de los tres comparta fila o columna con otro.
a cada vez que un número es mayor que otro que ocupa una posición posterior. Por ejemplo, la permutación (2 3 1) tiene dos inversiones, pues al comparar los tres números dos a dos, vemos que mientras 2<3, resulta que 2>1 y 3>1. La siguiente figura recoge las inversiones de cada permutación.
a cada vez que un número es mayor que otro que ocupa una posición posterior. Por ejemplo, la permutación (2 3 1) tiene dos inversiones, pues al comparar los tres números dos a dos, vemos que mientras 2<3, resulta que 2>1 y 3>1. La siguiente figura recoge las inversiones de cada permutación. | = (1 2 3) | |  | = (2 3 1) 2>1 3>1 | |  | = (3 1 2) 3>1 3>2 |
 | = (3 2 1) 3>2 3>1 2>1 | | 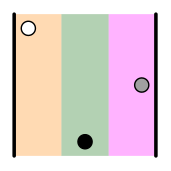 | = (1 3 2) 3>2 | | 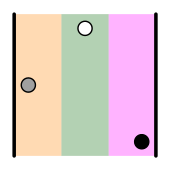 | = (2 1 3) 2>1 |
Los primeros tres productos tienen un número par de inversiones (0 o 2), mientras que los tres últimos tienen un número impar (1 o 3). Pues bien, los primeros conservarán su signo, mientras que a los segundos les cambiaremos el signo (esto se debe al teorema de Laplace, es decir, al resultado de desarrollar el determinante por una fila o una columna).
Como es fácil equivocarse de permutación, el matemático francés Sarrus ingenió una regla mnemotécnica que hoy lleva su apellido. Consiste simplemente en añadir las dos primeras filas al final de la matriz (o, alternativamente, las dos primeras columnas a la derecha de la matriz) y trazar tres diagonales de izquierda a derecha y otras tres en sentido contrario (a estas se les cambiará el signo), tal como muestra la siguiente construcción.
Observa que si imaginas que el "borde inferior" de la caja que ocupa el determinante coincide con el "borde superior", puedes mentalmente pasar del inferior al superior sin demasiado esfuerzo. Es como cuando en un videojuego un objeto que va desapareciendo por un lado de la pantalla va surgiendo por el lado opuesto. Este "juego mental" es lo que muestra la parte superior derecha de la construcción.
Geométricamente, al pegar dos lados opuestos de un cuadrado (la caja del determinante) sin girarlos, obtenemos un cilindro, que es lo que muestra la parte inferior derecha de la construcción.
Como ves, existen diversas variantes de la regla nemotécnica de Sarrus. ¡Elige la que más te guste!
ingenió una regla mnemotécnica que hoy lleva su apellido. Consiste simplemente en añadir las dos primeras filas al final de la matriz (o, alternativamente, las dos primeras columnas a la derecha de la matriz) y trazar tres diagonales de izquierda a derecha y otras tres en sentido contrario (a estas se les cambiará el signo), tal como muestra la siguiente construcción.
Observa que si imaginas que el "borde inferior" de la caja que ocupa el determinante coincide con el "borde superior", puedes mentalmente pasar del inferior al superior sin demasiado esfuerzo. Es como cuando en un videojuego un objeto que va desapareciendo por un lado de la pantalla va surgiendo por el lado opuesto. Este "juego mental" es lo que muestra la parte superior derecha de la construcción.
Geométricamente, al pegar dos lados opuestos de un cuadrado (la caja del determinante) sin girarlos, obtenemos un cilindro, que es lo que muestra la parte inferior derecha de la construcción.
Como ves, existen diversas variantes de la regla nemotécnica de Sarrus. ¡Elige la que más te guste!Autor de la actividad y construcción GeoGebra: Rafael Losada.