Le sezioni coniche
Vogliamo costruire le coniche di Apollonio. Partiamo dalla definizione di superficie conica.
Definizione: Data una retta r nello spazio che intersechi in V la retta a, si chiama superficie conica a due falde la superficie generata in una rotazione completa di r attorno ad a.
La parte di spazio racchiusa dalla superficie è detta cono a due falde.
La retta r, e ogni altra retta r’ della superficie conica, si dice generatrice.
L’angolo θ che r forma con a si chiama semiapertura.
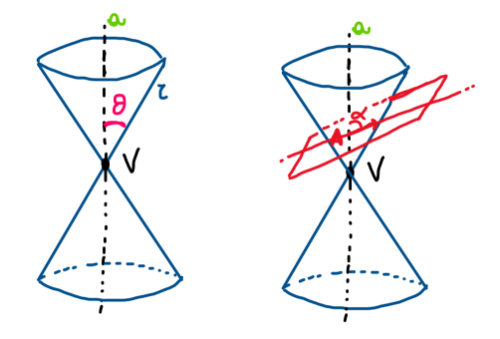
Costruiamo una superficie conica a due falde con vertice V(0,0,0), asse z e apertura variabile
Nella barra di inserimento scriviamo allora:
V=(0,0,0) vertice del cono
a=asseZ retta che rappresenta l'asse z
θ= 30° slider che costituirà la semiapertura del cono
InfiniteCone(V,a,θ) superficie conica a due falde
La parabola, la circonferenza, l’ellisse e l’iperbole sono dette sezioni coniche proprio perché tali curve si possono ottenere sezionando con un piano una superficie conica a due falde.
Sia α l’angolo che il piano secante forma con l’asse a del cono.
Costruiamo un piano passante per il punto A=(0,0,2) con inclinazione α.
Nella barra di inserimento scrivere:
A=(0,0,2) punto sull’asse z
α=30° slider che costituirà l’angolo di inclinazione del piano secante rispetto ad a
v=(0,sin(α),cos(α)) vettore che forma con a un angolo variabile α
f=Retta(A,v) retta passante per A e parallela al vettore v
g=Perpendicolare(A,f,pianoXY) retta passante per A e perpendicolare a f, e parallela al pianoXY
Piano(f,g) piano passante per le rette f e g
Utilizza ora il comanda INTERSECA SUPERFICI
per trovare l’intersezione tra il cono e il piano.
Fissa un valore di θ e fai variare α, cosa osservi?